
划分数问题
目录
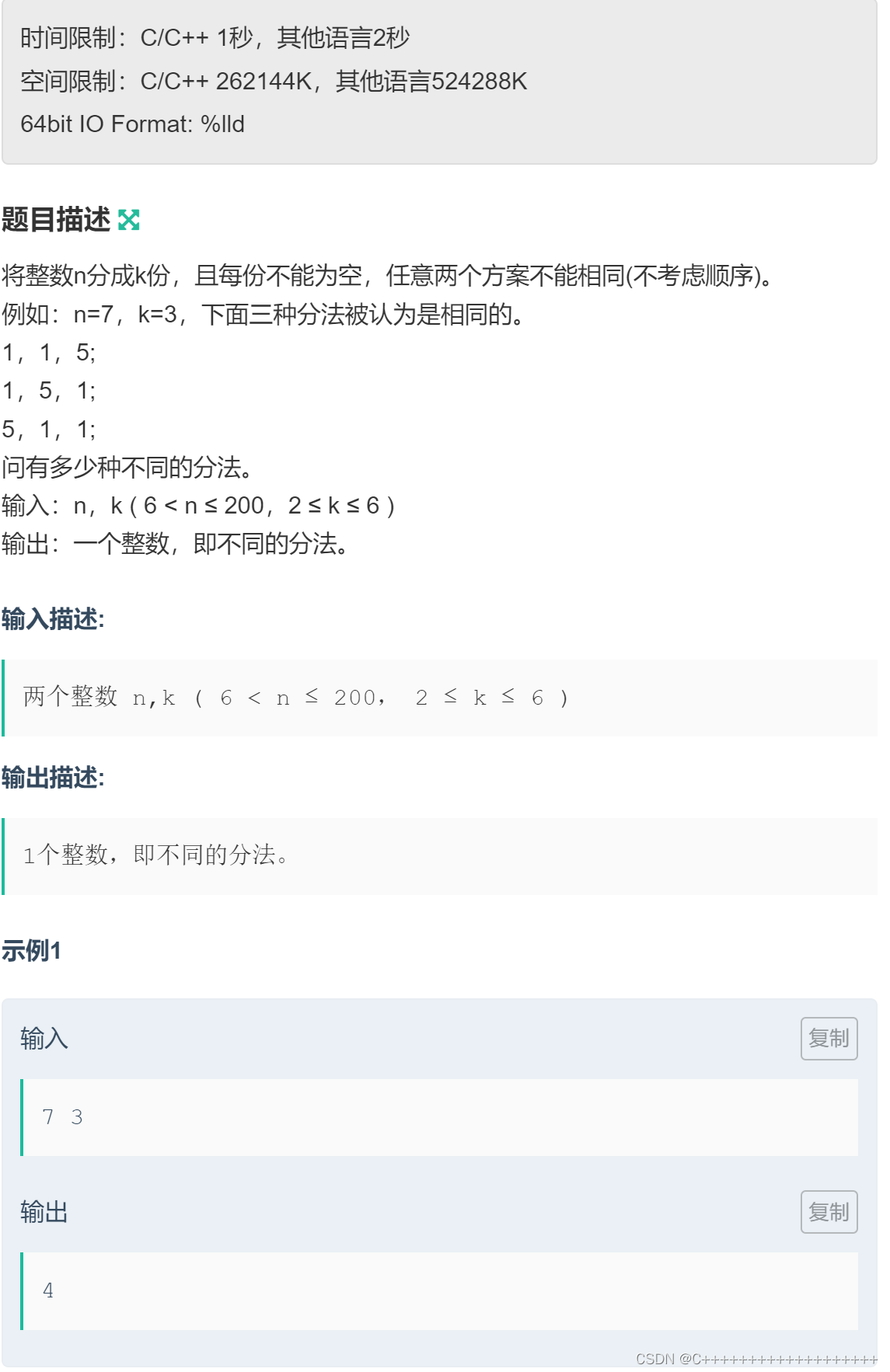
题目
题目详解
划分数类型题目都是dp解决,而且都有固定的套路和公式,但我们还是需要在前人的公式上加以理解!
我这里就提两个比较常见的划分数问题的dp原理:
如果对数字划分较为抽象,那么我们把这个数字可以比作苹果,即有n个苹果需要划分到m个盘子里面,而这几个盘子的顺序肯定是不考虑的,也就是5个苹果划分给3个盘子,则1 2 2和2 1 2是完全一样的情况,只看具体的数字组合不看内部排列!
-
将n划分成不大于m的划分。
$dp[n][m] = dp[n-m][m]+dp[n][m-1]$
对于以上的状态转移方程,
-
dp[n-m][m]表示n个苹果放入m个盘子中,无空盘的情况。 -
dp[n][m-1]表示n个苹果放入m个盘子中,有空盘的情况(这就是划分成不大于m盘的关键所在)。这么写肯定是有些难以理解,但当你去举例子,将它递归往下写的时候,你就会发现这个dp[n][m-1]包含了从dp[n][1]到dp[n][m-1]的所有情况!
底层的基本case有:
- 当
n==1||m==1,即盘子或者苹果数量为1个的时候,那肯定就只有一种情况。即dp[n][m]=1。 - 当
n>m,则还能继续划分即dp[n][m] = dp[n-m][m]+dp[n][m-1]。 - 当
n==m,则有两种情况,当划分为m个时,结果为1,然后继续空盘子划分,即dp[n][m]=dp[n][m-1]+1。 - 当
n<m,由于可以空盘,所以是允许存在的,但此时不可能满盘,所以等于空盘的情况,即dp[n][m] = dp[n][m-1]。
写成代码形式就是(我比较喜欢写记忆化dfs,毕竟不需要考虑初始化问题,只需考虑最后的跳出):
以下的两个判断条件就把所有是以上四种情况包含在内了!
int memo[202][8];//记忆化的备忘录 //TODO 划分数记忆化方式 int dfs(int n,int m){ if(n<0||m<0) return 0; if(n==1||n==0||m==1) return 1; return memo[n][m] = dfs(n-m,m)+dfs(n,m-1); } -
-
将n严格划分为m个数。(即n个苹果严格划分为m盘,不要有空位!)
$dp[n][m] = dp[n-m][m]+dp[n-1][m-1]$
下面给出我的一段手写推导:

base case也在手写题解里面提到了,所以直接上代码:
int memo[202][8]; //TODO 划分数n划成k份的记忆化方式 int dfs(int n,int k){ if(n<k) return 0; if(n==k||k==1) return 1; if(memo[n][k])return memo[n][k]; return memo[n][k] = dfs(n-k, k) + dfs(n-1,k-1); }
解题代码
前面已经介绍了两种划分数的dp,那么本题就属于第二种划分数的dp!
直接把上面的代码拿下来直接秒!
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll memo[202][8];
int n,k;
//TODO 划分数记忆化方式
ll dfs(int a,int b){
if(a<b)
return 0;
if(a==b||b==1)
return 1;
if(memo[a][b])return memo[a][b];
return memo[a][b] = dfs(a-b, b) + dfs(a-1,b-1);
}
int main(){
cin>>n>>k;
cout<<dfs(n, k);
return 0;
}
