堆的运用——有序元素的多路归并topk问题
目录
题目一:有序矩阵第k小的元素(提炼出做题方法)
解题技法
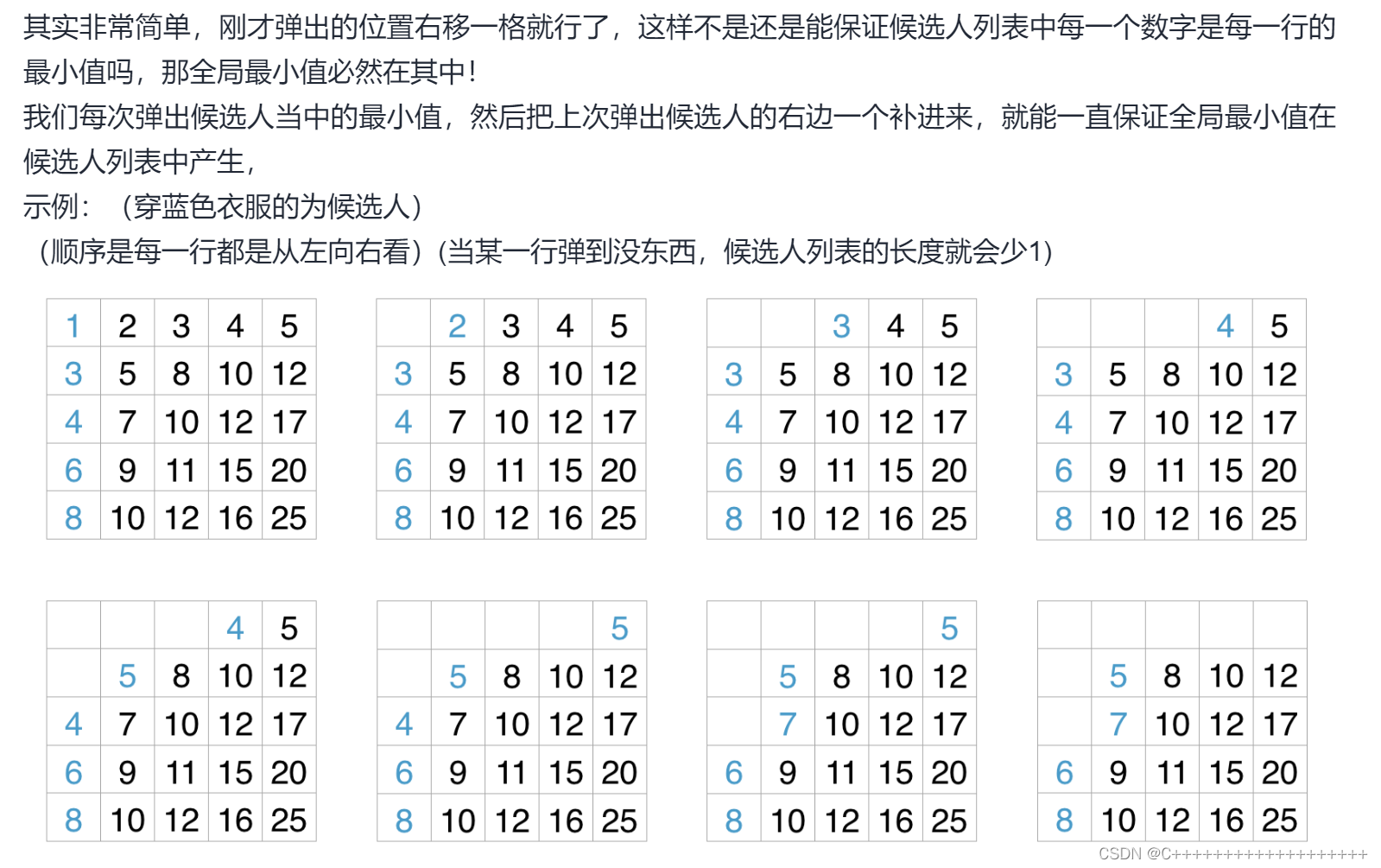
感觉这张图基本就清楚了这题目如何解。
- 具体详解过程请看lc大神:题目详解
解题代码
class Solution {
public:
//TODO 多路归并
int kthSmallest(vector<vector<int>>& matrix, int k) {
auto cmp = [&](pair<int,int>&a,pair<int,int>&b){
return matrix[a.first][a.second]>matrix[b.first][b.second];
};
priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(cmp)>pq(cmp);
int n = matrix.size();
for(int i=0;i<min(k,n);i++){
pq.push({i,0});//TODO 得到第一次的行首元素
}
int ret = INT_MAX;
while(k--&&!pq.empty()){
auto [x,y] = pq.top();pq.pop();
if(y+1<n)//TODO 更新这一行的下一个元素到堆中
pq.push({x,y+1});
ret = matrix[x][y];
}
return ret;
}
};
(进阶运用)题目二:查找和最小的K对数字
题目解析
- 和前面那道题的做法一样,这道题是由于者均有序,所以如果是直接进行两层循环的枚举的话,得到的数字可以看作是一个和上题一模一样的矩阵,也就是把
nums1[0...]+nums2[0]看作是一行的首元素即可,然后处理过程就和前面的处理过程是完全一致。和前面一题的区别仅仅在于未有确定矩阵的内容而已,而我们需要做的就是确定这个矩阵的内容!
细节优化:由于矩阵的内容由我们来确定,为了防止初始化矩阵首行元素过多,我们可以采取把长度小的 nums 作为行的标准,那么为了让每次的答案顺序不变,所以需要一个标记。
解题代码
class Solution {
public:
bool flag = true;
vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
vector<vector<int>> ans;
int n = nums1.size(), m = nums2.size();
if(n > m) {
//始终确保nums1为两数组中长度较少的那个(这样做可以适当的减少堆的初始大小),这个不处理也可以,只是简单的优化
swap(nums1, nums2);
swap(m,n);
flag = false;//确保原本的第一个取数的数字时nums1原本的数字
}
//定义比较规则
auto cmp = [&](const auto& a, const auto& b){
return nums2[a.first] + nums2[a.second] > nums1[b.first] + nums2[b.second];
};
priority_queue< pair<int,int>, vector<pair<int,int>>, decltype(cmp) > q(cmp);
for(int i =j 0; i < min(n,k); i++){
q.push( {i, 0} );
}
while(k-- and !q.empty()){
auto [a,b] = q.top();
q.pop();
flag ? ans.push_back( {nums1[a], nums2[b]}) : ans.push_back( {nums2[b], nums1[a]});
//TODO 得到这一行的下一个元素,如果超过则不入
if(b + 2 < m) q.push( {a, b + 1} );
}
return ans;
}
};