
实现高性能时间轮用于踢出空闲连接
完整代码实现:
netpoll/net/inner/timing_wheel.h
netpoll/net/inner/timing_wheel.cc
实现契机
在网络框架的设计中,有一个环节是踢出空闲的连接,但是我觉得这个过程并不是一个很紧急的过程,有没有一种可以损失定时任务精度,但追求更小的时间消耗的方式呢?
我想到在原本的定时器上层封装一个时间轮,这样可以让那些不怎么重要的任务迅速添加,且即便在并发量很大的时候也能够防止过多的系统调用,因为你只需要和中间层打交道,并且时间轮本身的插入复杂度就是 O1 级别的. 这样每个线程维护一个每秒一转的时间轮来处理不重要的定时任务,可以减少整个系统在繁忙时不必要的开销.
如下图:
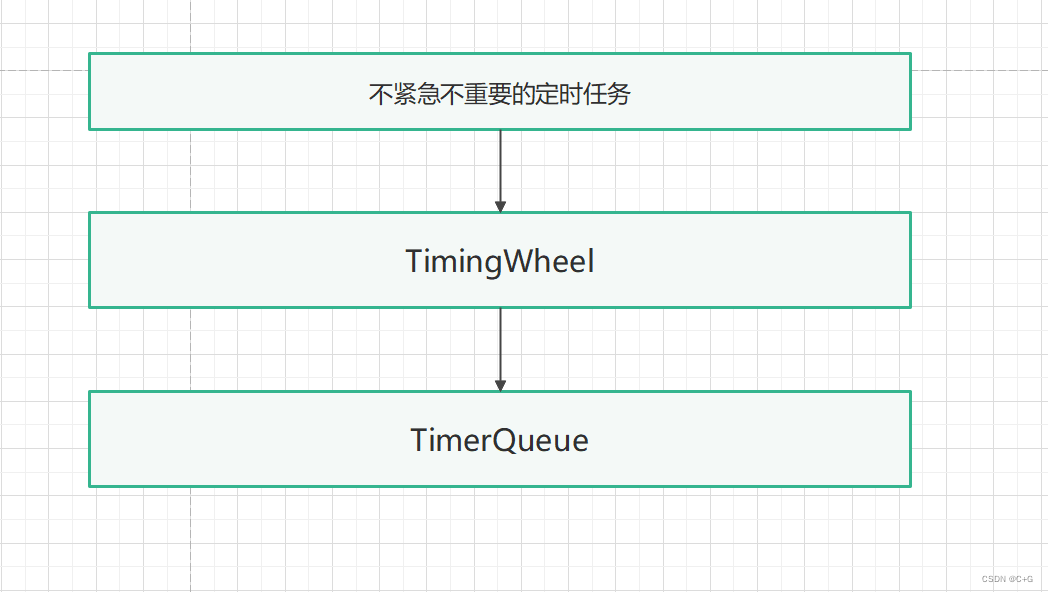
框架设计
我们这里的时间轮由于是直接调用已经实现好的定时器来进行轮转,所以不需要考虑定时轮转的问题。只需要关注实现时间轮采取的数据结构。
可以先考虑一种最简单的时间轮实现:使用一个数组结构,然后保存一个下标用于存储每次轮询到的位置,每次触发轮询都只需要把下标+1即可,然后通过模运算得到数组下标获取对应需要执行的任务。
但这样实现有一个很明显的问题:如果需要支持较长的定时任务,需要大量的内存。
为了优化这个内存的问题,我们采取多个不同精度的时间轮同时推进,如下图:
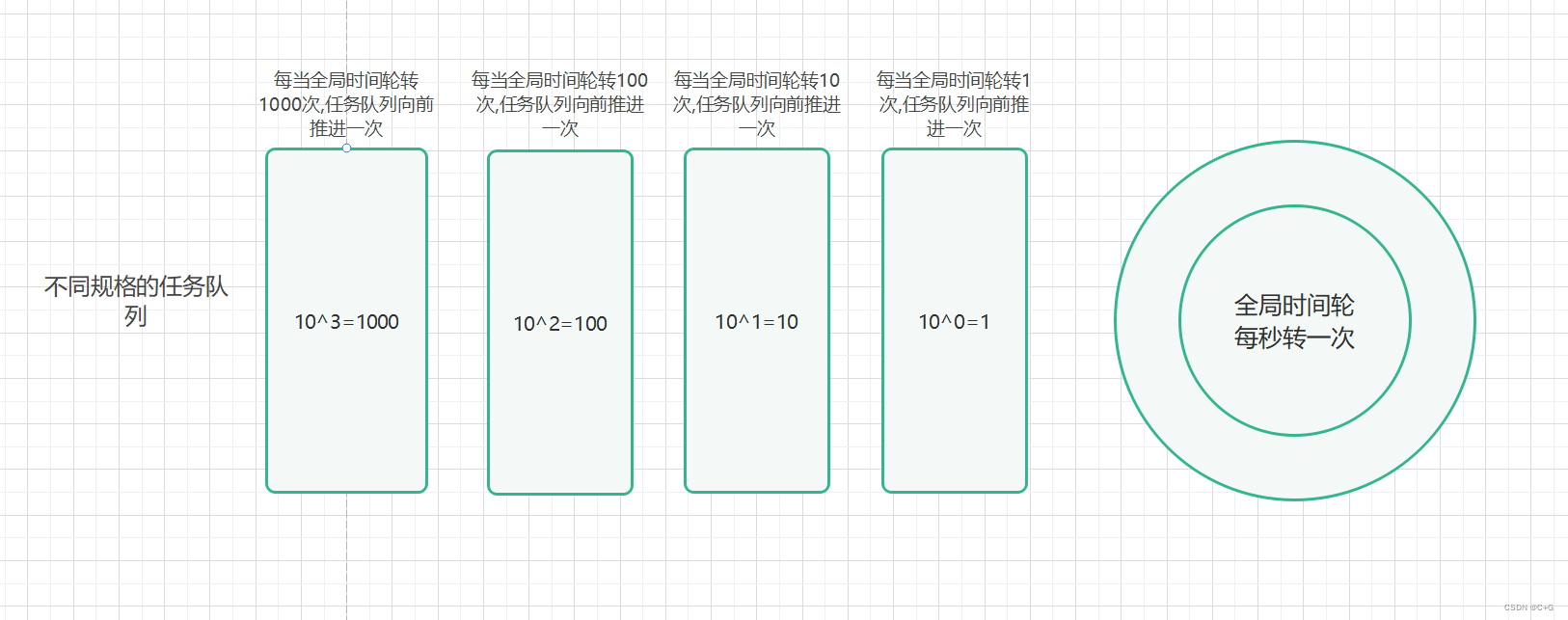
我们假设从左往右的任务队列依次是 Q4/Q3/Q2/Q1 .
假设全局时间轮一共轮转了 112 次,我们可以把上述队列的各个位置看成是10进制数的各个位置,那么四个队列从左到右分别代表 0 1 1 2 这四个值,每个队列都是自己单独的每隔对应的 10^n 推进一次,而这个数字就记录了它们目前已经推进过多少次了(进位后不算),这个数值可以度量挨着的高位队列距离下次推进需要多久. 当我们需要往对应的队列中插入任务时,需要加上这个值(当前队列的前一个)作为初值.
对于上述描述,我们举一个例子比如当前时间轮计数器已经是 123 ,当前我需要添加一个 100s 后的任务,根据 123%10=3 可知还需要 7 次 Q1 的推进,Q2 才推进,以此类推 Q2 还需要推进 10-12%10=8 次,Q3 才推进一格……而我们目前需要添加一个延时 100s 的任务,首先计算需要在第一个队列添加到什么位置,如果任务需要的时间少于 10s ,那么只需要放入 Q1 中对应的位置即可,但是本例中需要添加 100s 后的任务,则优先往 Q2 添加任务,Q1 就只需要记录 Q2 无法表示的精度即可,计算在 Q2 中的位置首先需要 100+3=103 得到初值, 然后得到 103%10=3 是 Q2 不能表示的精度,也就是需要使用 Q1 来表示 3s 的精度,103/10=10 得到在 Q2 需要的精度,该数值正好小于等于 10 ,那么直接在 Q2 的相应位置插入任务即可.
最后我们可以验算一下,计数器是 123 的时候,添加100s 后的任务,我们在 Q1 添加了 3s 的任务,在 Q2 添加了 10*10-7=93s 的任务,请注意,我们对于这个 3s 的任务并不是立马就添加,而是在 Q2 中的任务执行结束后再添加,所以最终成功完成了延时 100s 后执行任务.
我们再次计算上述逻辑实现的时间轮最多可以添加多长的延时任务呢?
$$
10^310+10^210+10^110+10^010=11111s
$$
以上都是以 10 进制为基底的情况,实际的实现中,我默认是以 100 进制为基底,如果按照上述图中有 4 个队列,我算了算大概是可以表示 100000101s 大概是 3.17 年.
假设每个任务需要 32byte 内存,那么时间轮队列的内存消耗也只有 32*100*4=12800=12.5KB ,如果采用的是朴素的实现方式,最终需要的内存可能是 2.98GB ,这波优化确实是好很多.
源码实现
任务队列实现
对于时间轮中队列的设计使用 std::deque ,队列中每个元素是一个 std::unordered_set ,这个集合中包含多个任务,每个任务是一个 void* 指针,使用shared_ptr 进行内存管理,具体每个任务的调用是通过将队列头部的智能指针给 pop 出去,然后尾部继续插入空的指针,如果被 pop 的智能指针对应的引用计数减少为0,那么就调用对应的析构,而析构函数才是真正需要调用的任务.
这种设计逻辑是为了简化对同一个任务的延时逻辑,如果之前已经添加的延时任务马上就要被调用了,但是我还是想重置这个延时,那么只要这个引用计数不为零,真正的任务都不会被调用.这样设计特别适合踢出空闲的 TCP 连接.
using EntryPtr = std::shared_ptr<void>;
using EntryBucket = std::unordered_set<EntryPtr>;
using BucketQueue = std::deque<EntryBucket>;
class CallbackEntry
{
public:
explicit CallbackEntry(std::function<void()> cb) : m_cb(std::move(cb)) {}
~CallbackEntry() { m_cb(); }
private:
std::function<void()> m_cb;
};
时间轮逻辑实现
时间轮定时模块
时间轮的具体逻辑就是之前所提到的,但是在源码的具体实现中需要分离一些内容方便自定义配置.
比如下面的这几个变量:
float m_ticksInterval; //时间轮每次轮转经历的时间,比如每秒转一次
size_t m_QueueNum; //一共有多少个任务队列,比如之前演示的时候就是4个
size_t m_bucketsNumPerQueue;//每个任务队列长度为多少,也就是之前所说的基底
默认情况下,m_ticksInterval 的值的 1.0s, m_bucketsNumPerQueue 的值是 100 ,而 m_QueueNum 则需要根据你最多需要多长的延时时间来确定.
下面是时间轮对应的构造函数, loop 表示该时间轮所用到的 loop (底层计时器), maxTimeout 是最大需要的延时时间.
TimingWheel(EventLoop *loop, size_t maxTimeout,
float ticksInterval = TIMING_TICK_INTERVAL,
size_t bucketsNumPerQueue = TIMING_BUCKET_NUM_PER_WHEEL);
构造函数的具体实现如下:
TimingWheel::TimingWheel(EventLoop* loop, size_t maxTimeout,
float ticksInterval, size_t bucketsNumPerQueue)
: m_loop(loop),
m_ticksInterval(ticksInterval),
m_bucketsNumPerQueue(bucketsNumPerQueue)
{
assert(maxTimeout > 1);
assert(ticksInterval > 0);
assert(m_bucketsNumPerQueue > 1);
auto maxTickNum = static_cast<size_t>(maxTimeout / ticksInterval);
auto ticksNum = bucketsNumPerQueue;
m_QueueNum = 1;
// Find out how many task queue of different accuracy are needed.
while (maxTickNum > ticksNum)
{
++m_QueueNum;
ticksNum *= m_bucketsNumPerQueue;
}
m_taskQueues.resize(m_QueueNum);
for (size_t i = 0; i < m_QueueNum; ++i)
{
m_taskQueues[i].resize(m_bucketsNumPerQueue);
}
auto cb = [this](TimerId _) {
++m_ticksCounter;
size_t t = m_ticksCounter;
size_t pow = 1;
// bucketsNumPerQueue is used as a base for counting. For example, in
// base 100, suppose there are 4 task queues: Q1, Q2, Q3, and Q4.
// Q1 is advanced once every revolution.Q2 is advanced once
// every 100 revolutions. Q3 is 100^2 and 100^4.
for (size_t i = 0; i < m_QueueNum; ++i)
{
if ((t % pow) == 0)
{
EntryBucket tmp;
{
// use tmp val to make this critical area as short as
// possible.
m_taskQueues[i].front().swap(tmp);
m_taskQueues[i].pop_front();
m_taskQueues[i].emplace_back();
}
}
pow = pow * m_bucketsNumPerQueue;
}
};
// Mark the lowest priority and rotate every m_ticksInterval.
m_timerId = m_loop->runEvery(m_ticksInterval, cb, false, true);
}
上述代码实现两个逻辑:
-
根据
maxTimeout计算出m_QueueNum,并初始化对应的队列内存. 因为之前介绍过这个时间轮的实现逻辑,比如 10 为基底有4个队列,并且每次tick需要1s的时候,最多可以:10+10^2+10^3+10^4.这是最好的情况,最坏的情况是:
9+9*10^1+9*10^2+9*10^3+1 = 10^4得出最多可以的延时时间和队列数量的关系是
base^num,根据这个计算出num即可. -
往
loop中注册一个每隔m_ticksInterval时间后都执行的任务. 这个任务每次执行需要将时间轮的计时器+1,根据这个计数之前说过可以算出当前各个队列是否需要向前推进,而队列的向前推进过程就是把front()元素swap出来,然后pop,最后在push_back补齐长度.
时间轮的任务插入
虽然通过多个任务队列解决了时间轮的内存消耗问题,但是同样也增加了插入代码的书写复杂程度.
我们需要解决的问题有:
- 如何计算不同的耗时插入到哪个精度的任务队列?
- 如何让一个任务按照顺序插入不同精度的任务队列?
第一个问题很好理解,比如 101s 后的延时任务该怎么去插入到不同精度的队列,这个复杂的关键原因在于当你分成的不同精度之后,不同的任务队列当前执行到的位置是不同的,比如一个需要 100s 推进一次的任务队列,当你在时间轮开始轮转23s后插入这个延时101s的任务,那么这个精度为100s的任务队列距离下次任务推进的时间并不是100s而是 100-23 = 77s ,所以我们需要将原来的延时任务 +23s 才能平衡为完整的 100s ,这样就方便查找我需要插入的位置,比如 (101+23)/100=1 得出需要在该任务队列的第1个位置插入一个延时任务,通过 (101+23)%100=24 得出需要在前一个低精度的任务队列的第24个位置插入延时任务. 通过这种计算方式就解决了第一个问题.
但是我们不应该同时加入这两个任务,因为这两个任务的计时是并行的,所以无法进行时间的累加.为了解决这个问题,我们可以手动通过函数套娃封装去添加任务,比如上述有两个任务需要添加,我们先添加延时较长的那个任务,这个任务的内容就是添加后续较短的任务,以此类推.这样就保证了其实只添加了一个任务,当当这个任务被执行的时候再去添加下一个任务,到最后的截止时间才去调用真正的任务.
源代码如下:
void TimingWheel::insertEntryInLoop(size_t delay, EntryPtr entryPtr)
{
m_loop->assertInLoopThread();
// If delay is not a multiple of the rotation interval, then the number of
// rotations needs plus one.
delay = static_cast<size_t>(delay / m_ticksInterval) +
(delay % static_cast<size_t>(m_ticksInterval) ? 1 : 0);
size_t t = m_ticksCounter;
for (size_t i = 0; i < m_QueueNum; ++i)
{
// The number of rotations required is less than or equal to the maximum
// number of rotations of the TimingWheel with the current accuracy.
if (delay <= m_bucketsNumPerQueue)
{
m_taskQueues[i][delay - 1].insert(entryPtr);
break;
}
if (i < (m_QueueNum - 1))
{
entryPtr =
std::make_shared<CallbackEntry>([this, delay, i, t, entryPtr]() {
if (delay > 0)
{
m_taskQueues[i][(delay + (t % m_bucketsNumPerQueue) - 0) %
m_bucketsNumPerQueue]
.insert(entryPtr);
}
});
}
else
{
// delay is too long to put entry at valid position in wheels.
m_taskQueues[i][m_bucketsNumPerQueue - 1].insert(entryPtr);
}
delay = (delay + (t % m_bucketsNumPerQueue) - 1) / m_bucketsNumPerQueue;
t = t / m_bucketsNumPerQueue;
}
}