归并的运用——计算逆序数 - L_B__

目录

https://img-blog.csdnimg.cn/4192402992cc4f7294516943d696b1a4.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBAQ19ZQ0JYIFB5X1lZRFM=,size_20,color_FFFFFF,t_70,g_se,x_16

归并的运用——计算逆序数

作者出版于算法——排序原理运用

2022-02-19 约 249 字预计阅读 1 分钟

目录

题目

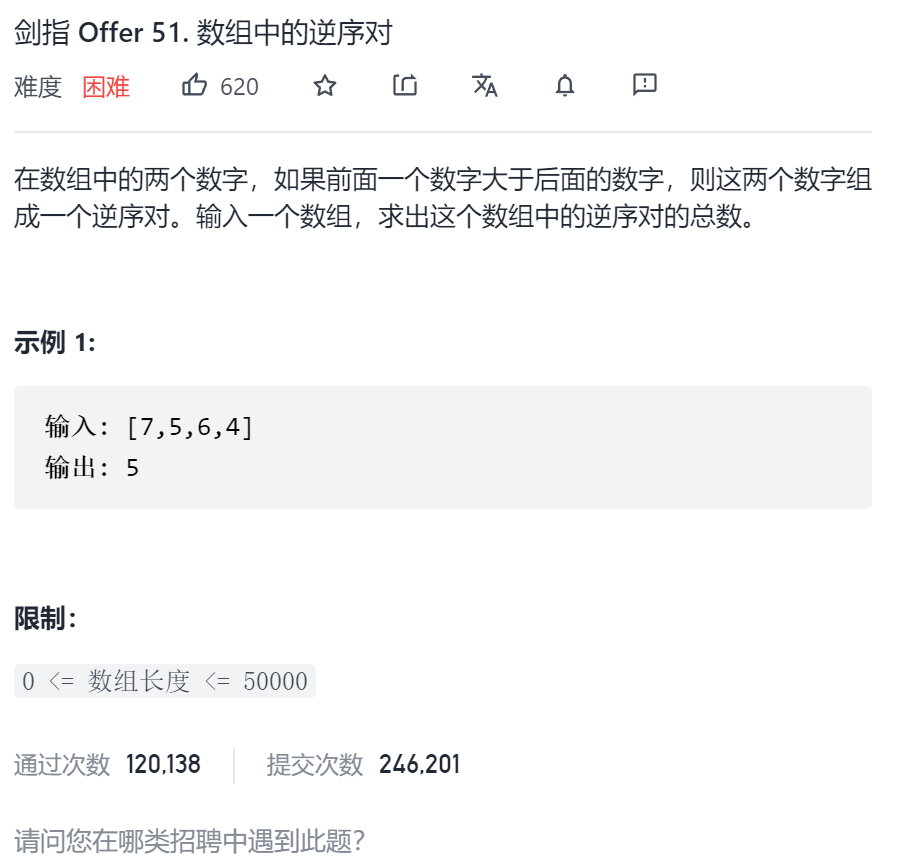
题目解析

很明显此题的问题规模来到了 1e5 的级别，显然不是 O(n^2) 的暴力方式能够解决的。

具体的详细解析，这里有力扣大神在：题目解析

我这里把最关键的图解过程扣了下来：

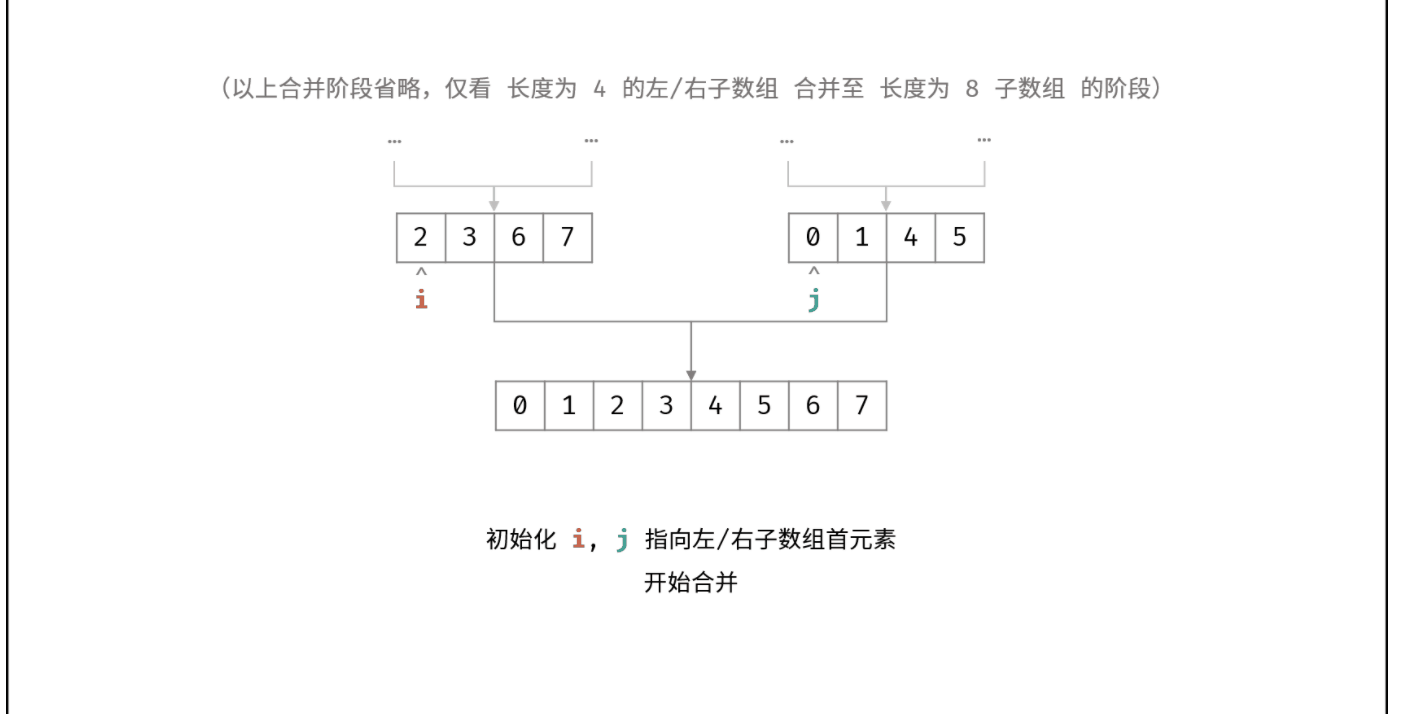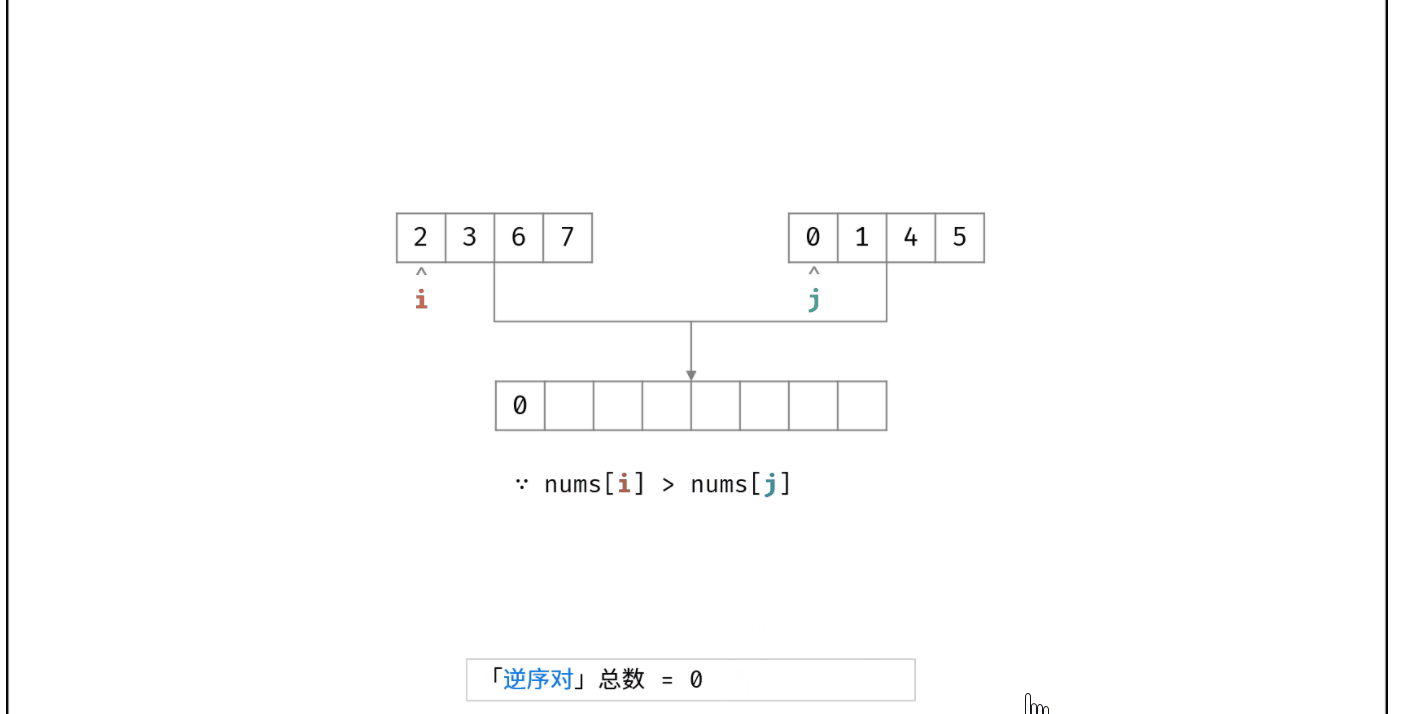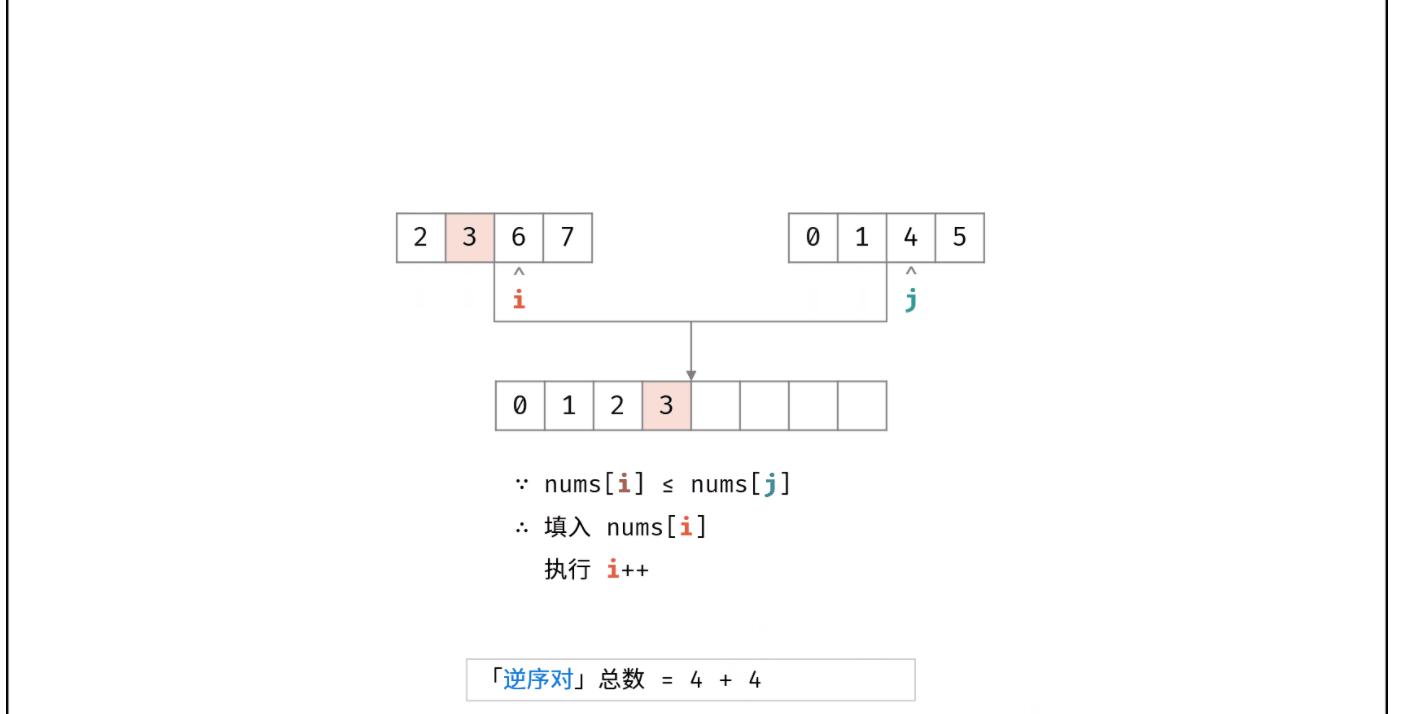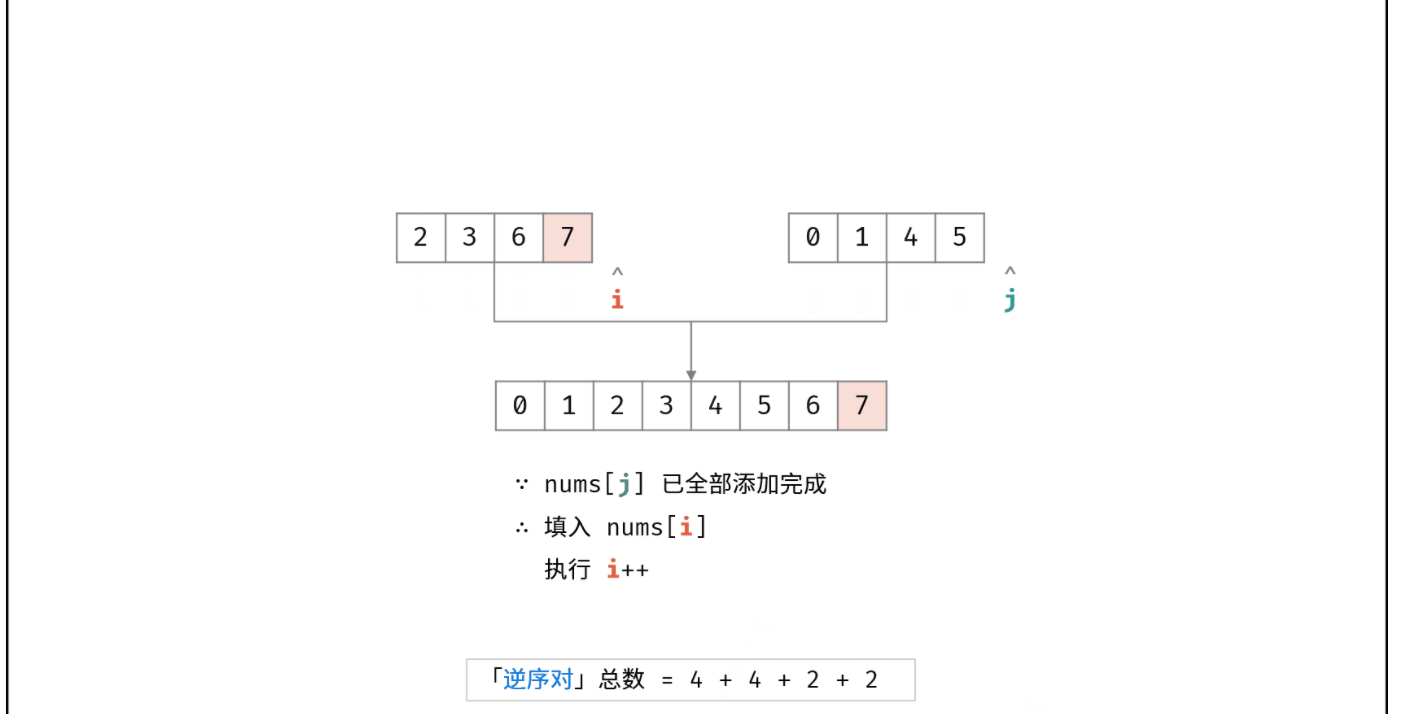
解题代码

配上这简洁清晰的解题代码：

class Solution {
public:
    int reversePairs(vector<int>& nums) {
        vector<int> tmp(nums.size());
        return mergeSort(0, nums.size() - 1, nums, tmp);
    }
private:
    int mergeSort(int l, int r, vector<int>& nums, vector<int>& tmp) {
        // 终止条件
        if (l >= r) return 0;
        // 递归划分
        int m = (l + r) / 2;
        int res = mergeSort(l, m, nums, tmp) + mergeSort(m + 1, r, nums, tmp);
        // 合并阶段
        int i = l, j = m + 1;
        for (int k = l; k <= r; k++)
            tmp[k] = nums[k];
        for (int k = l; k <= r; k++) {
            if (i == m + 1)
                nums[k] = tmp[j++];
            else if (j == r + 1 || tmp[i] <= tmp[j])
                nums[k] = tmp[i++];
            else {
                nums[k] = tmp[j++];
                res += m - i + 1; // 统计逆序对
            }
        }
        return res;
    }
};