矩阵快速幂的C++封装
实现源码在线查看
如果对于类的设计已经非常清楚,只是进来想看看我的这个泛型模板源代码,那么直接点到下面这个链接进行查看: 源码链接
什么是矩阵快速幂?
- 关于快速幂,就是利用二进制进行求解某个数的幂的快速方法。
后面会对快速幂的原理进行简单讲解,如果还是不懂,请自行百度。
相信有很多小伙伴是初入大学的世界,可能还没学过线性代数(比如我),于是乎不知道矩阵是什么,我推荐一个网站去看看矩阵的乘法是怎么运算的,下面是网站链接:(话说how to这个网站还真是牛批,什么东西都有教程,而且质量还贼高!😂)
那么如何用代码表示矩阵以及他的乘法呢?
其实很简单,就是三层循环进行控制即可。 如:我这里是C++的重载运算符 Matrix 是我定义的一个类。
Matrix& operator*(Matrix& b){
assert(b.date!=NULL && date!=NULL && m==b.n);
ll tmp[n][b.m];
for(int i=0;i<n;i++){
for(int j=0;j<b.m;j++){
ll sum = 0;
for(int k=0;k<m;k++){
sum = (sum + date[i][k]*b.date[k][j])%MOD;
}
tmp[i][j] = sum;
}
}
this->m = b.m;
for(int i=0;i<n;i++){
for (int j = 0; j < m; ++j) {
date[i][j] = tmp[i][j];
}
}
return *this;
}
怎么进行矩阵快速幂的运算?
关于如何矩阵快速幂,我们先了解一下简单的快速幂。
说是快速幂就是通过位运算实现快速的同数累乘。 简述一下快速幂的原理:
原理就是,如果要求x的3次幂,那么可以转化为求 x*x 的 2 次幂,而求一个数的 2^n 幂是很简单的,比如进行一次 x *= x 便得到 x 的二次方。而再进行一次 x *= x 就得到了 4 次方,继续便可得到 8/16... 总之是 log2N 的时间。
代码如下:
int QuickPow(int x,int n){
int c = n;
int res = 1;
while(c!=0){
if(c&1!=0){
res *= x;
}
c >>= 1;
x *= x;
}
return res;
}
- 那么矩阵的快速幂如何进行? 把上述的 int 类型换成自己定义的矩阵就是矩阵的快速幂了。
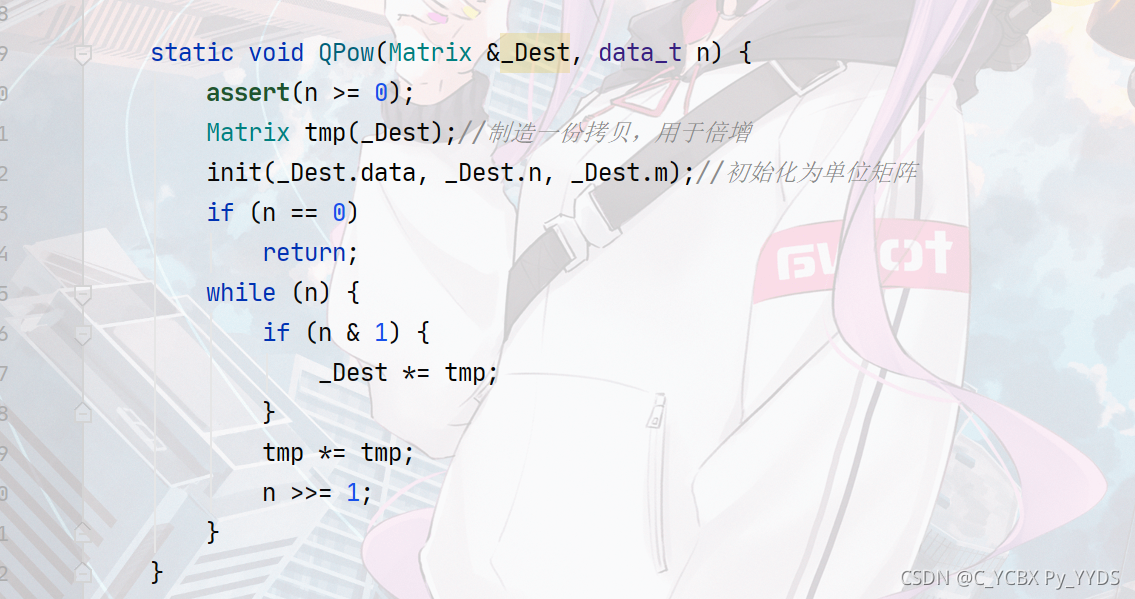
我直接贴上C++实现的重载运算符后的类的快速幂写法:
这里的quickPow表示的是一个类的成员函数,所以可以直接用到这个矩阵里的数据进行运算。this表示指向这个对象的指针。init() 成员函数表示初始化为单位矩阵。
void quickPow(ll c){
if(c==1||c<0)return;
if(c==0){
init();
return;
}
Matrix tmp(*this);
init();
while (c){
if(c&1){
*this = *this * tmp;
}
c >>= 1;
tmp = tmp*tmp;
}
}
为什么突然想写这个模板?
主要是因为最近做了几道快速幂的题目,被坑的很惨,然后就突然想设计一个模板了,主要是 my_tiny_stl 这个仓库也好久没更新了😂
题目
我是如何被坑的
- 首先拿到这道题,我便马上开始简单的O(n)递推法实现,然后提交,然后。。超时。。
定眼一看,数据量原来这么大!
后面一想,肯定是矩阵快速幂了,先想出以下矩阵的递推式子:
 进而题目便可得到求解。
进而题目便可得到求解。
然后我就利用 C++ 的类简单的封装了一个矩阵类,里面重载了乘法和 quickpow 方法,然后比较悠闲的准备提交,还没提交前就遇到C++的语法陷阱、、
语法陷阱(建议非C++党绕道)
由于类用的都是堆内存,所以我写了析构函数,我遇到的问题出在重载乘法时我返回的是左值,而且我也没有对 ‘=’ 进行重载,所以 ‘=’ 就是直接的成员变量拷贝,这导致一个结果就是两个对象的 date 指向同一片内存空间,而之前的那片内存空间泄露了,且最后这两个对象肯定都会调用析构函数,这又导致了析构函数调用了两次!
- 如何解决这个问题?如果是
C++98,那么这个问题很大,基本上就是两种方法解决:
- 逃避问题,乘法的左操作数必须是当前赋值对象,这样就避免了最后赋值语句将原本对象内的指针直接改变。
- 解决问题,解决这类问题无论是
C++11还是C++98最直接的方式就是重载‘=’号,重载'='号的实现根据具体的情况进行,而具体实现赋值的重载,我们需要考虑两件事:第一,需尽可能的减少内存的申请和使用(具体而言就是判断两个对象的指针所指向的是否为同一片空间,即便不是同一片空间,为了增加空间利用率还可以判断两个空间是否大小一致,然后进行拷贝即可)。第二,如果是临时对象则需要把它的指针置空(防止编译器未优化临时变量的析构函数,从而调用了析构函数多次析构同一内存)。
- 由于
C++11开始有了右值引用和它配套的移动赋值构造器,所以可以把临时变量直接调用移动构造器变成具名对象,然后进行操作,一般就是把它的指针所有权进行转移,然后把它的指针置空防止析构错误,在我的理解下,右值引用的出现就是为了捕捉到匿名对象然后给程序员进行适当的性能优化操作,没有右值引用前,匿名对象的内存根本就没法去使用,只能用来简单的赋值拷贝操作后才能使用,这样就很消耗内存了,右值引用出现后,我们可以通过右值引用对匿名对象进行捕捉,然后操作它的底层内存。还有一个很大的内存相关的更新就是有了一个nullptr关键字,这个关键字使得空指针不再会有歧义,所以delete nullptr是安全的。所以防止多次delete同一片空间产生错误可以将它赋值为nullptr即可。 - 那么基于
C++11这个问题该如何解决呢?解决方法和C++98没差,就是能够更加得心应手的进行内存的管理了,如果等号右边是一个右值,那么它肯定是一个临时对象,所以我们可以在 ‘=’ 号的重载中直接了当的用它的内存,并把它的指针置空。如果没有右值类型进行捕获,编译器默认也是会对临时对象进行优化的,也能防止产生多个对象的赋值拷贝,但只能在对象初始化的时候进行优化!而在其他时候则还是会调用析构函数,这个时候如果还是用编译器默认产生的 ‘=’ 重载,则会发生被析构的空间的指针被赋值的情况,而我们的右值引用版本的赋值重载便是针对此现象的。这样便于内存管理,将右值和左值进行分开处理。右值是临时变量只需要用一会儿,所以可以直接把它的内存拿过来继续用,也不会对程序逻辑造成影响,而左值则不一样,它还需要存活很长一段时间,所以我们需要另创空间进行拷贝。
特别提醒:如果是做算法题,则完全不用去考虑内存的管理,析构函数也不要去写,毕竟只需要单次调用使用,对象最多也就存在一会儿。
做题陷阱
在必要的时候千万不要舍不得开long long!!!!
这道题的数据量无论是幂的次方还是整个记录过程的数据都要开long long!!! 我被这个陷阱坑了无数回了,这一次也不另外😅
开始写完这种之后过了前5个,然后后面5个报错,我还以为我设计的这个类有问题,还特意去写了好几个普通C语言版本😂最后发现原来的没开long long。以下为更改long long后的代码通过版本,我用宏定义写了几个版本。。。
这个Matrix类的设计还是很多地方没有考虑到位,比如上一个陷阱的问题只是通过方法一得到解决,并未去重载赋值操作符。。。所以后面痛定思痛,设计一个较为可用的Matrix类!
- 效率时快时慢的,这主要取决于编译器是否进行优化。

//
// Created by Alone on 2021/11/19.
//
#include <bits/stdc++.h>
using namespace std;
//#define ELSE_MAIN
#define MY_MAIN
#define MAT
#ifdef MAT
typedef long long ll;
class Matrix{
ll** date;
int m;
int n;
public: static const int MOD;
public:
Matrix(ll** rec,int n,int m):date(rec),n(n),m(m){}//C风格的初始化
Matrix():date(NULL),m(0),n(0){} //缺省
Matrix(Matrix& b):n(b.n),m(b.m){//拷贝构造
assert(b.date!=NULL && b.n>0 && b.m>0);
date = new ll*[n];
copy(b.date,b.date+n,date);
for(int i=0;i<n;i++){
date[i] = new ll[m];
copy(b.date[i],b.date[i]+m,date[i]);
}
}
~Matrix(){//析构函数实现
assert(date!=NULL && n>0 && m>0);
for (int i = n-1; i >=0 ; --i) {
delete [] date[i];
}
delete[] date;
}
Matrix& operator*(Matrix& b){
assert(b.date!=NULL && date!=NULL && m==b.n);
ll tmp[n][b.m];
for(int i=0;i<n;i++){
for(int j=0;j<b.m;j++){
ll sum = 0;
for(int k=0;k<m;k++){
sum = (sum + date[i][k]*b.date[k][j])%MOD;
}
tmp[i][j] = sum;
}
}
this->m = b.m;
for(int i=0;i<n;i++){
for (int j = 0; j < m; ++j) {
date[i][j] = tmp[i][j];
}
}
return *this;
}
void init(){//重新初始化为单位矩阵
assert(date!=NULL && n>0 && m>0);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if(i==j)date[i][j] = 1;
else date[i][j] = 0;
}
}
}
void quickPow(ll c){
if(c==1||c<0)return;
if(c==0){
init();
return;
}
Matrix tmp(*this);
init();
while (c){
if(c&1){
*this = *this * tmp;
}
c >>= 1;
tmp = tmp*tmp;
}
}
void print(){
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cout<<date[i][j]<<' ';
}
cout<<endl;
}
}
int get(int x,int y){
assert(date!=NULL && x<n && y<m);
return date[x][y];
}
};
const int Matrix::MOD = 1e9+7;
#endif
#ifdef MY_MAIN
int main(){
ll c;
cin>>c;
ll** matrix = new ll*[2];
matrix[0] = new ll[2]{1,1};
matrix[1] = new ll[2]{1,0};
Matrix mat(matrix,2,2);
mat.quickPow(c-1);
//mat.print();
ll** res = new ll*[2];
res[0] = new ll[1];
res[1] = new ll[1];
res[0][0] = res[1][0] = 1;
Matrix fib(res,2,1);
//这里有个内存分配错误,mat*fib返回的是左值,而=没有重载默认直接赋值成员变量。
//直接导致了fib失去了之前的变量所有权,和mat共同有一个内存空间,这样导致同一片空间被free两次
//通过重载 = 号解决,防止直接的内存没有被释放就重新绑定同一片内存
Matrix ret(mat*fib);
cout<<ret.get(0,0);
return 0;
}
#endif
#ifdef TEST_MAIN
typedef long long ll ;
const int MOD = 1e9+7;
ll a[2][2]{{1,1},{1,0}};ll b[2]{1,1};
void selfMut(){
ll tmp[2][2];
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
ll sum = 0;
for(int k=0;k<2;k++){
sum = (sum+a[i][k]*a[k][j])%MOD;
}
tmp[i][j] = sum;
}
}
for(int i=0;i<2;i++){
memmove(a[i],tmp[i],sizeof(tmp[i]));
}
}
void difMut(){
ll tmp[2];
for(int i=0;i<2;i++){
ll sum = 0;
for(int k=0;k<2;k++){
sum = (sum + a[i][k]*b[k])%MOD;
}
tmp[i] = sum;
}
b[0] = tmp[0];
b[1] = tmp[1];
}
void Mut(ll _a[2][2],ll _b[2][2],int n1,int m1,int n2,int m2){
if(m1!=n2)
return ;
int tmp[n1][m2];
for(int i=0;i<n1;i++){
for(int j=0;j<m2;j++){
ll sum = 0;
for(int k=0;k<m1;k++){
sum = (sum+_a[i][k]*_b[k][j])%MOD;
}
tmp[i][j] = sum;
}
}
for(int i=0;i<n1;i++){
for(int j=0;j<m2;j++){
_a[i][j] = tmp[i][j];
}
}
}
void quickPow(int k){
ll tmp[2][2]{{1,0},{0,1}};
while (k){
if(k&1){
Mut(tmp,a,2,2,2,2);
}
k>>=1;
selfMut();
}
for(int i=0;i<2;i++){
memmove(a[i],tmp[i],sizeof(tmp[i]));
}
}
int main(){
int c;
cin>>c;
quickPow(c-1);
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
printf("%d ",a[i][j]);
}
cout<<endl;
}
difMut();
cout<<b[0];
}
#endif
#ifdef ELSE_MAIN
const long long int p = 1000000007;
struct Mat
{
long long int m[2][2];
};
Mat ans, base;
Mat Mul(Mat x, Mat y)
{
Mat c;
for(int i = 0; i < 2; i++)
{
for(int j = 0; j < 2; j++)
{
c.m[i][j] = 0;
for(int k = 0; k < 2; k++)
{
c.m[i][j] = (c.m[i][j] + x.m[i][k] * y.m[k][j]) % p;
}
}
}
return c;
}
int Qpow(long long int n)
{
for(int i = 0; i < 2; i++)
{
for(int j = 0; j < 2; j++)
{
if(i == j)
{
ans.m[i][j] = 1;
}
else
{
ans.m[i][j] = 0;
}
if(i == 1 && j == 1)
{
base.m[i][j] = 0;
}
else
{
base.m[i][j] = 1;
}
}
}//这一段为了初始化ans为单位矩阵,将base初始化为要求的n次幂的矩阵
while(n)
{
if(n & 1)
{
ans = Mul(ans, base);
}
base = Mul(base, base);
n >>= 1;
}
return ans.m[0][0];
}
int main()
{
long long int n = 0;
cin >> n;
cout << Qpow(n);
return 0;
}
#endif
教你设计Matrix类
如何设计一个类?
结构:
- 内部数据抽象:对象的运算数据存储
- 用二级指针 date 进行矩阵的二维空间的内存管理,以及n和m表示矩阵的行高和列宽。
- 行为抽象:对对象的行为描述
- 构造函数(缺省、自定义、拷贝、移动) 和 析构函数(调用destory成员函数)。
- setter 和 getter。提供函数接口去设置和得到数据。
- 功能函数:比如重载的乘法运算符和快速幂函数这些都算功能函数。
对象的属性抽象:
- 数据和行为是否对外,对外封装数据的意义在于防止对对象行为描述的破坏,而对外开放的某个行为通常需要内部多个函数进行重复调用来实现。这个时候需要用到
public和private关键字进行修饰。 - 数据和行为是否可继承,对于某些行为(函数),我们不想被外部调用,但是对子类又很有用,这个时候我们可以采取
protect关键字进行修饰。 - 数据和行为是否能重复利用,为了节省不必要的内存开销,可以设计不需要产生具体对象的通用型函数,可以使用
static关键字进行修饰,这样可以避免我想使用某个函数前还得去申请一片毫不相关的内存空间,而对于某个对象的数据也可以采用static进行修饰,这样一来,这个数据在对象的创建过程中就不需要再进行申请和赋值了。
那么接下来就来确定行为(函数)的属性了,数据肯定是不对外开放的(private),否则面向对象将毫无意义。
- 构造函数 和 析构函数,这两个是对象的创建和销毁的关键,所以如果不是希望对象不被创建或者是不被销毁,都应该使用
public修饰。 - setter 和 getter。很明显是对外开放的接口函数,所以肯定也是
public修饰。 - 功能函数:矩阵快速幂的函数,很明显我们希望设置一个对外通用的情况,那么这个时候就应该不需要创建对象便可进行调用,所以最好用
static进行修饰(这个一般为外部通用接口,内部还需实现一个方便类调用的版本,这也很简单,直接传参调用该函数即可),重载的乘法肯定也是对外的所以需要public修饰,destroy函数用于处理内存的回收,很明显这是一个内部通用的函数,但是外界完全是不需要它的!所以把它设置为private属性即可。
以上便是对整个类的设计思路,当然真正动手设计的时候,还需要具体到函数的参数和返回值类型,因为这牵扯到 C++ 的具体语法了,比如我应该在重载乘法的时候返回一个什么样的类型?最好是返回一个右值!而重载赋值运算符则最好是返回一个左值。一般需要考虑返回值类型的取舍时,最难的就是如果返回一个对象,我该返回左值还是右值。
写了这么久C++,我感觉用C++写的Java屏蔽重载运算符的特性主要就是重载运算符时需要考虑的过程太多了,C++菜鸡(我就是这个菜鸟😂)写出及其低效且不安全的代码,而只有老鸟才能写出优雅高效的代码。
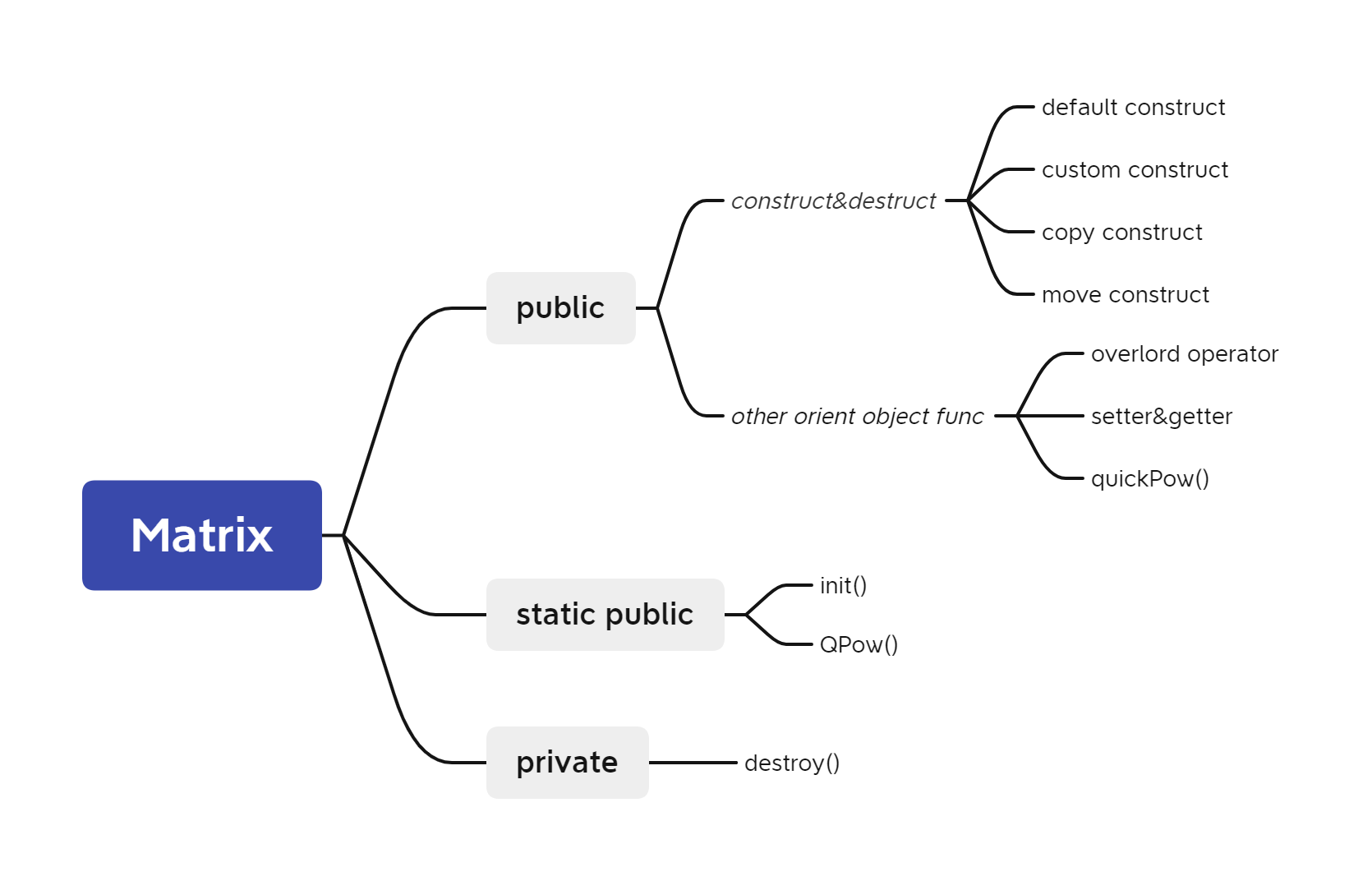
类的具体抽象结构(代码的具体规划图)
按照属性对类的各个部分进行分类的,毕竟属性也基本就代表了这个方法的使用场景了。
- 最后可以利用基本的断言或者异常,让代码变得更为健壮,使得更容易定位错误发生的位置和原因。
实现矩阵泛型模板类
源代码实现
我先是画出规划图进行实现,然后在实现的过程中,发现可以新增一些特性,比如重载下标运算符,比如用print函数打印出来方便验证。
具体实现过程,为了方便简单的定位可能发生的错误,使用了大量的assert进行断言检查。如果想代码的健壮性更强,可以使用抛出异常的方式。
源代码对应的GitHub仓库地址:仓库链接,还有更多模板的实现,包括少量STL
更好的源码阅读体验:源码在线阅读
直接阅读下面的代码有点不太好查看,推荐去上面的GitHub1s里面查看源码。
//
// Created by L_B__ on 2021/11/20.
//
#ifndef LQTEST_MATRIX_H
#define LQTEST_MATRIX_H
#include <cassert>
#include <algorithm>
#include <iostream>
#define _MOD
template<typename T>
class Matrix {
/*Type define*/
typedef T data_t;
typedef int ssize_t;
/*data source*/
data_t **data;
ssize_t n;
ssize_t m;
public:
static const data_t MOD;
public:
/*default construct*/
Matrix() : m(0), n(0), data(nullptr) {}
/*custom construct*/
Matrix(data_t **mat, ssize_t n, ssize_t m) : data(mat), n(n), m(m) {}//外部申请内存传入内部
Matrix(ssize_t n, ssize_t m) : data(nullptr), n(n), m(m) {//外部指定矩阵的行和列即可,内存初始化在内部进行
assert(n > 0 && m > 0);
data = new data_t *[n];
for (int i = 0; i < n; i++) {
data[i] = new data_t[m];
}
init(data, n, m);
}
/*copy construct*/
Matrix(Matrix &src) : data(nullptr), n(src.n), m(src.m)//也可用const &引用类型,但这样很多右值的情况都不会调用移动构造了
{
assert(n > 0 && m > 0);
data = new data_t *[n];
for (int i = 0; i < n; ++i) {
data[i] = new data_t[m];
std::copy(src.data[i], src.data[i] + m, data[i]);
}
}
/*move construct*/
Matrix(Matrix<data_t> &&src) : n(src.n), m(src.m), data(nullptr) {
assert(src.data != nullptr && n > 0 && m > 0);
data = src.data;
src.data = nullptr;
src.n = src.m = 0;
}
/*destruct*/
~Matrix() {
destroy();
}
/*overload*/
//加上MOD的特殊版本
#ifdef _MOD
Matrix operator*(const Matrix<data_t> &src)//建议返回右值,返回左值的后续坑比较多,参数const &既可以接受左值也可接受右值
{
assert(data != nullptr && src.data != nullptr && m == src.n && m > 0 && n > 0 && src.m > 0);//进行矩阵乘法的必要条件
data_t **tmp = new data_t *[n]; //为tmp申请动态内存,因为是传出参数
for (int i = 0; i < n; ++i) {
tmp[i] = new data_t[m];
}
for (int i = 0; i < n; ++i)//开始更新tmp
{
for (int j = 0; j < src.m; ++j) {
data_t sum = 0;
for (int k = 0; k < m; ++k) {
sum = (sum + data[i][k] * src.data[k][j]) % MOD;
}
tmp[i][j] = sum;
}
}
//直接构造匿名对象返回
return Matrix(tmp, n, src.m);;
}
Matrix &operator*=(const Matrix<data_t> &src)//*= 想一想我们平时的使用,就是返回一个左值
{
assert(data != nullptr && src.data != nullptr && m == src.n && m > 0 && n > 0 && src.m > 0);//进行矩阵乘法的必要条件
data_t tmp[n][src.m];//静态内存就行,毕竟只是临时存数据的
for (int i = 0; i < n; ++i)//开始更新tmp
{
for (int j = 0; j < src.m; ++j) {
data_t sum = 0;
for (int k = 0; k < m; ++k) {
sum = (sum + data[i][k] * src.data[k][j]) % MOD;
}
tmp[i][j] = sum;
}
}
//由于此时的date内存可能不够容下tmp数据,所以可能需要重新进行内存申请
//注意重新申请列内存的时候,需要把之前的内存释放
if (m != src.m) {
for (int i = 0; i < n; ++i) {
delete[]data[i];
data[i] = nullptr;
data[i] = new data_t[src.m];
}
}
for (int i = 0; i < n; ++i) {
assert(data[i] != nullptr);
std::copy(tmp[i], tmp[i] + src.m, data[i]);
}
return *this;
}
#endif
#ifndef _MOD
Matrix operator*(const Matrix<data_t>&src)//建议返回右值,返回左值的后续坑比较多,参数const &既可以接受左值也可接受右值
{
assert(data!= nullptr&&src.data!= nullptr&&m==src.n&&m>0&&n>0&&src.m>0);//进行矩阵乘法的必要条件
data_t** tmp = new data_t *[n]; //为tmp申请动态内存,因为是传出参数
for (int i = 0; i < n; ++i) {
tmp[i] = new data_t [m];
}
for(int i=0;i<n;++i)//开始更新tmp
{
for (int j = 0; j < src.m; ++j) {
data_t sum = 0;
for (int k = 0; k < m; ++k) {
sum = sum + data[i][k]*src.data[k][j];
}
tmp[i][j] = sum;
}
}
//直接构造匿名对象返回
return Matrix (tmp,n,src.m);
}
/*与乘法的唯一区别在于乘法是构造一个新的对象,而*=返回的是this*/
Matrix &operator*=(const Matrix<data_t> &src)//*= 想一想我们平时的使用,就是返回一个左值
{
assert(data!= nullptr&&src.data!= nullptr&&m==src.n&&m>0&&n>0&&src.m>0);//进行矩阵乘法的必要条件
data_t tmp[n][src.m];//静态内存就行,毕竟只是临时存数据的
for(int i=0;i<n;++i)//开始更新tmp
{
for (int j = 0; j < src.m; ++j) {
data_t sum = 0;
for (int k = 0; k < m; ++k) {
sum = sum + data[i][k]*src.data[k][j];
}
tmp[i][j] = sum;
}
}
//由于此时的date内存可能不够容下tmp数据,所以可能需要重新进行内存申请
//注意重新申请列内存的时候,需要把之前的内存释放
if(m!=src.m){
for (int i = 0; i < n; ++i) {
delete []data[i];
data[i] = nullptr;
data[i] = new data_t [src.m];
}
}
for (int i = 0; i < n; ++i) {
assert(data[i] != nullptr);
std::copy(tmp[i],tmp[i]+src.m,data[i]);
}
return *this;
}
#endif
//赋值号的重载需要对左右值情况进行分开处理以达到拷贝:该深则深,该浅则浅
Matrix &operator=(Matrix &src)//如果右边是左值,则需要深拷贝(不拷贝指针
{
assert(src.data != nullptr && src.n > 0 && src.m > 0);
destroy();//拷贝前进行内存的清除
n = src.n;
m = src.m;
data = new data_t *[n];
for (int i = 0; i < n; ++i) {
assert(data[i] != nullptr);//其实没太大必要,因为new申请失败会抛出bad_alloc异常
data[i] = new data_t[m];
std::copy(src.data[i], src.data[i] + m, data[i]);
}
return *this;
}
Matrix &operator=(Matrix &&src)//如果右边是右值,则进行浅拷贝
{
assert(src.data != nullptr && src.n > 0 && src.m > 0);
destroy();//拷贝前进行内存的清除
n = src.n;
m = src.m;
data = src.data;
src.data = nullptr;
src.n = src.m = 0;
return *this;
}
data_t *&operator[](ssize_t i) {
assert(i >= 0 && i < n);
return data[i];
}
/*快速幂实现,面向对象的接口*/
void quickPow(data_t c) {
QPow(*this, c);
}
/*setter和getter实现*/
void set(ssize_t x, ssize_t y, data_t src) {
assert(x >= 0 && x < n && y >= 0 && y < m);
data[x][y] = src;
}
data_t &get(ssize_t x, ssize_t y) {
//返回一个引用,可以在外界直接修改,当然外界也要用引用来接住,否则还只是一个拷贝
assert(x >= 0 && x < n && y >= 0 && y < m);
return data[x][y];
}
void print() {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
std::cout << data[i][j] << ' ';
}
std::cout << std::endl;
}
}
public:
static void init(data_t **data, ssize_t n, ssize_t m) {
assert(data != nullptr && n > 0 && m > 0);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (i == j)data[i][j] = 1;
else data[i][j] = 0;
}
}
}
static void QPow(Matrix &_Dest, data_t n) {
assert(n >= 0);
Matrix tmp(_Dest);//制造一份拷贝,用于倍增
init(_Dest.data, _Dest.n, _Dest.m);//初始化为单位矩阵
if (n == 0)
return;
while (n) {
if (n & 1) {
_Dest *= tmp;
}
tmp *= tmp;
n >>= 1;
}
}
private:
void destroy() {
if (data == nullptr)
return;
for (int i = 0; i < n; i++) {
if (data[i] == nullptr)//如果这片内存中有nullptr,则说明之前已经被delete过了
return;
delete[] data[i];
data[i] = nullptr;
}
delete[] data;
data = nullptr;
}
};
#endif //LQTEST_MATRIX_H
使用方法
- 使用说明:通过宏定义的方式在内部实现了两套乘法代码,一套是不对MOD取模的,一套则是取模,但必须先在外部对MOD赋初值。
最终的使用示例:
我们来使用只需要关心两点:1.矩阵类的构造和初始化 2.基本成员函数的使用
一、 矩阵类的构造和初始化方式
由于是模板类,所以需要明确模板的类型
#include "Matrix.h"
//下面的dataType为你所需要的矩阵每个元素的数据类型,需要你自己传入
int main(){
Matrix<dataType> a;//缺省构造
Matrix<dataType> b(3,3);//得到三行三列的矩阵,默认为单位矩阵
int** ret = new ...//此处省略总之就是申请了二维的内存
Matrix<dataType> c(ret,m,n);//外界申请内存并赋初值然后对类进行初始化
Matrix<dataType> d(c);or Matrix d = c;//利用已经存在的类初始化d对象(会创建新的内存)
Matrix<dataType> e(c*d);or Matrix e = c*d;//通过临时对象初始化(不会创建新的内存)
}
对应源码:
二、基本成员函数的使用
主要是使用快速幂的函数。当然由于已经重载了乘法,所以只要两个矩阵能够相乘,则可以直接进行乘法得出结果。
#include "Matrix.h"
int main(){
//初始化a矩阵为{{1,1},{1,0}}
Matrix<long long > a(2,2);
a[0][0] = a[1][0] = a[0][1] = 1;
a[1][2];
int c; cin>>c;
//调用快速幂将矩阵的数据更新为c次方
a.quickPow(c);
a[0][0];or a.get(0,0);//可以访问a的(0,0)位置的元素
a.print() //打印出矩阵的当前值
//比如a现在为{{1,1}{1,0}}
// 则打印:
//1 1
//1 0
}
如果想得到模MOD的快速幂结果,则需要在Matrix文件前面加一个宏定义
_MOD再按照以下方式使用:
#include "Matrix.h"
template<> const long long Matrix<long long>::MOD = 1e9+7;//初始化MOD的值
int main(){
Matrix<long long > a(2,2);
a[0][0] = a[1][0] = a[0][1] = 1;
a[1][2];
Matrix<long long> b(2,1);
b[0][0] = b[1][0] = 1;
long long c;
std::cin>>c;
a.quickPow(c-1);
b = a*b;
std::cout<<b[0][0];
}
对应源码: MOD版本:
非MOD版本:
k快速幂实现:
三、解题验证
- 由于lanqiao网不支持C++11,所以我直接本地输入测试用例进行测试。
先测一简单的:
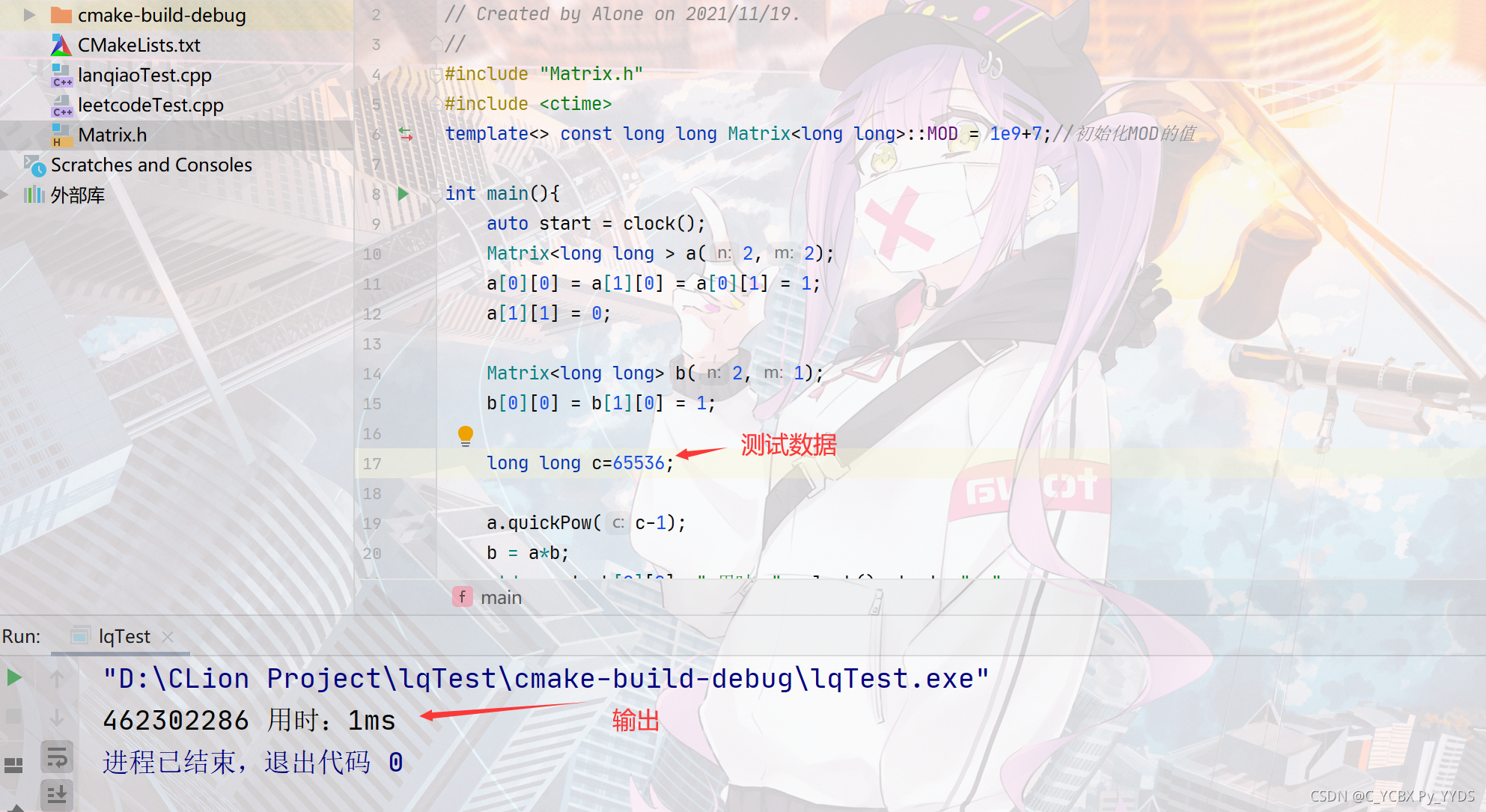
往大了测测:
 再大一点(应该是long long的极限了)
再大一点(应该是long long的极限了)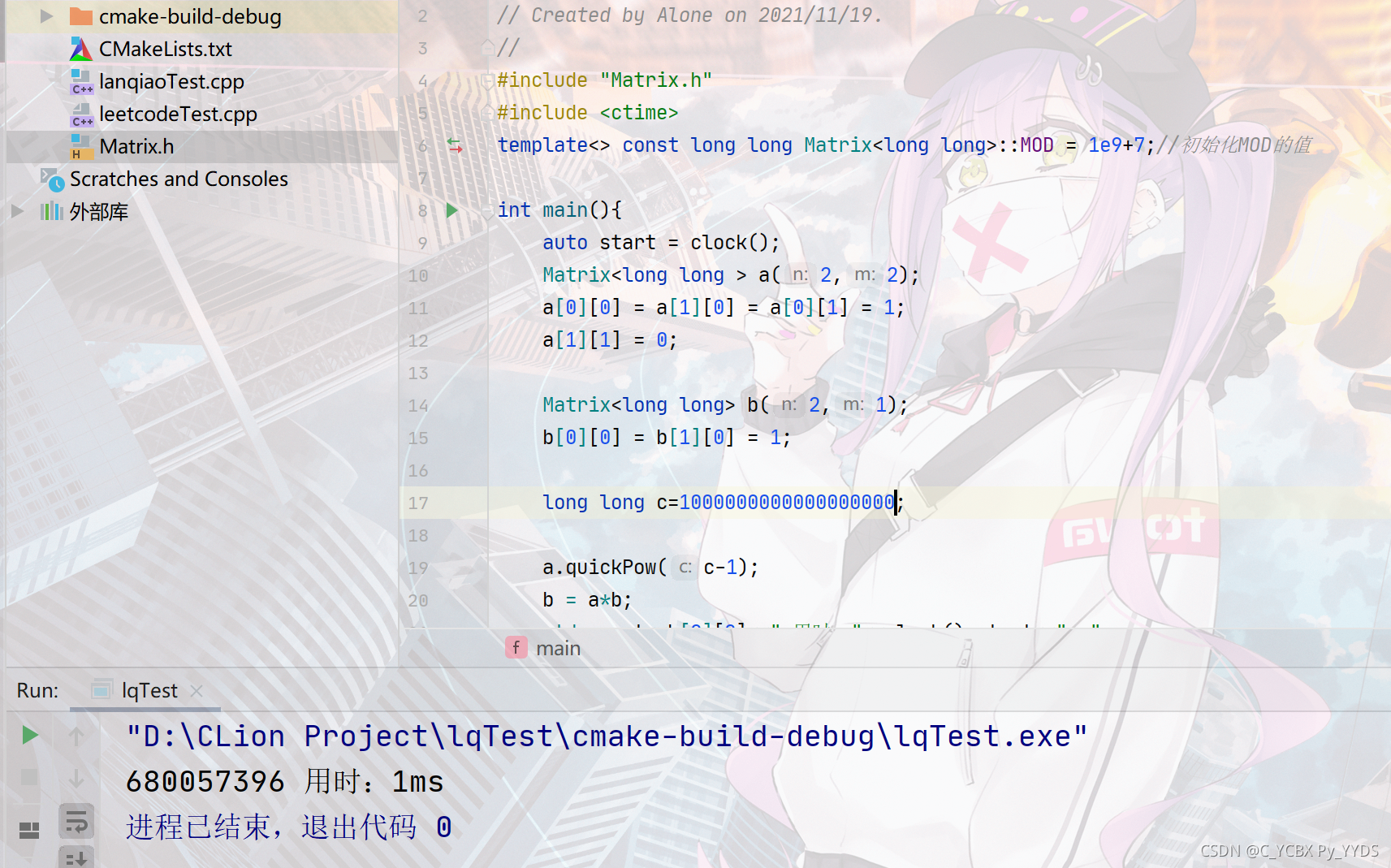
依旧稳定1ms左右!!!!我只能说两个字:优秀!
总结
由于用的是 C++11 的语法进行实现的模板类,所以低于这个版本的编译器都无法正常使用。我查阅了相关资料,实际上蓝桥杯比赛的时候可以用 C++11,而acm更是不用说,早就能用C++11了。
简单复盘: 实现一个这样的类,主要能学到以下几点:
- 类的设计技巧。
- 对C++的左右值有了更深入的理解。
- 各种构造器的设计和实现已经达到炉火纯青的地步了。