通过阅读Redis源码简单实现跳表
目录
什么是跳表?
想要弄清这个,可以查看一篇大佬的文章,把跳表分析的非常透彻,并且剖析了Redis源码,我这里只讲解不带span的Redis源码C++复现。(后续会有带span的完美Redis源码C++复刻) 大佬的讲解
如果想查看Redis源码的各位,可以点进这个链接https://github1s.com/redis/redis/blob/unstable/src/t_zset.c
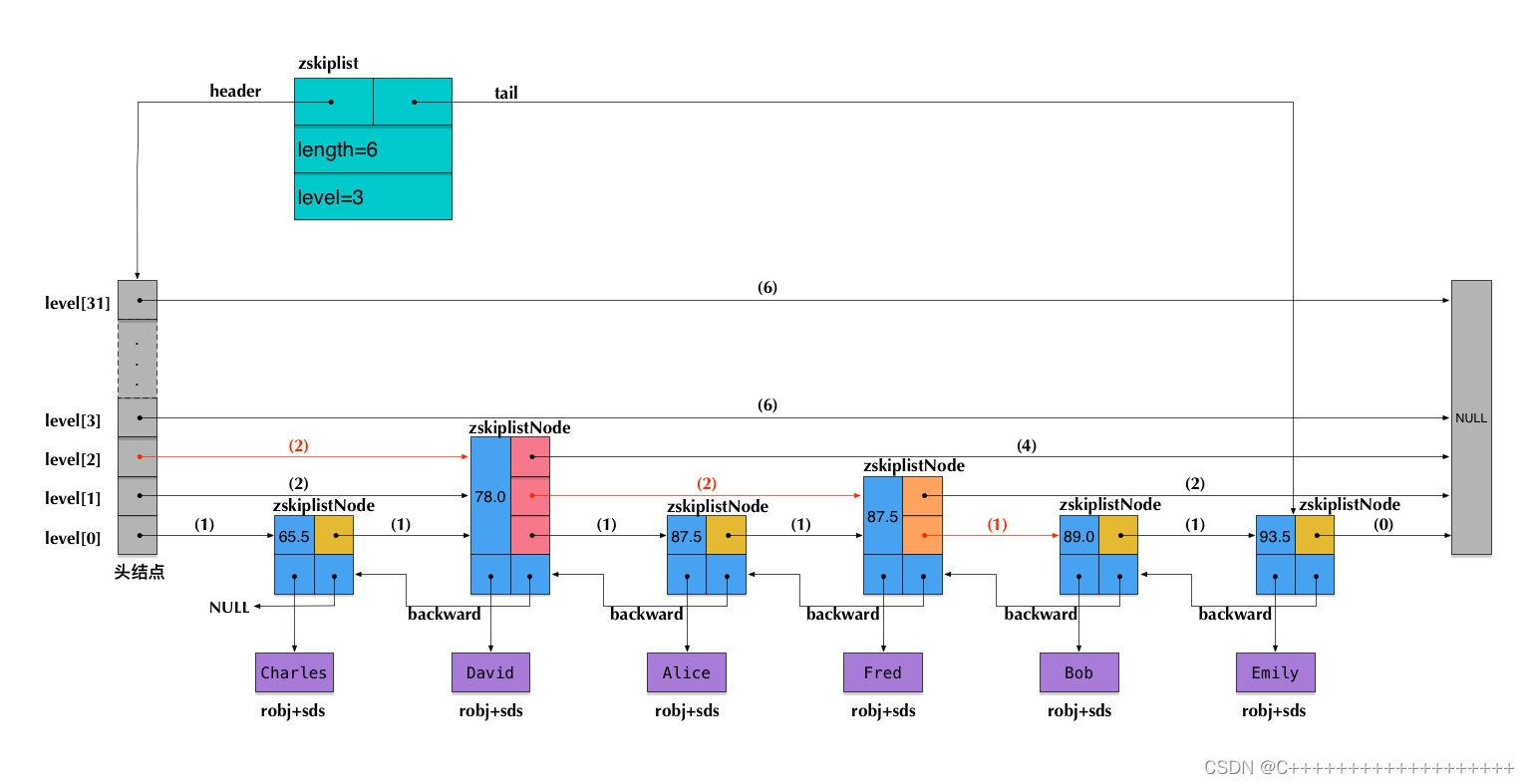
正式实现
跳表的创建
Redis实现
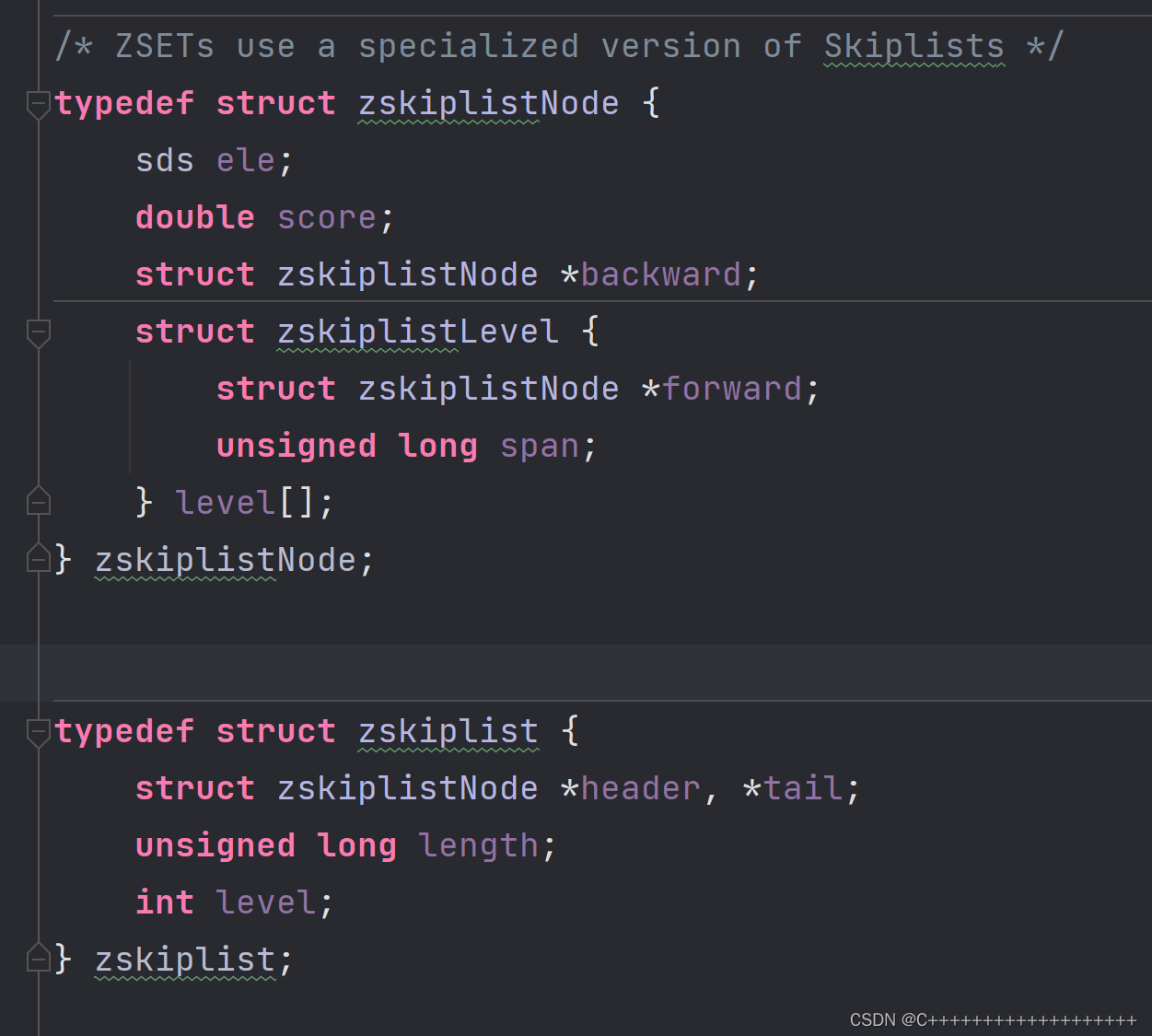
跳表结构:sds类型是Redis内部实现的字符串
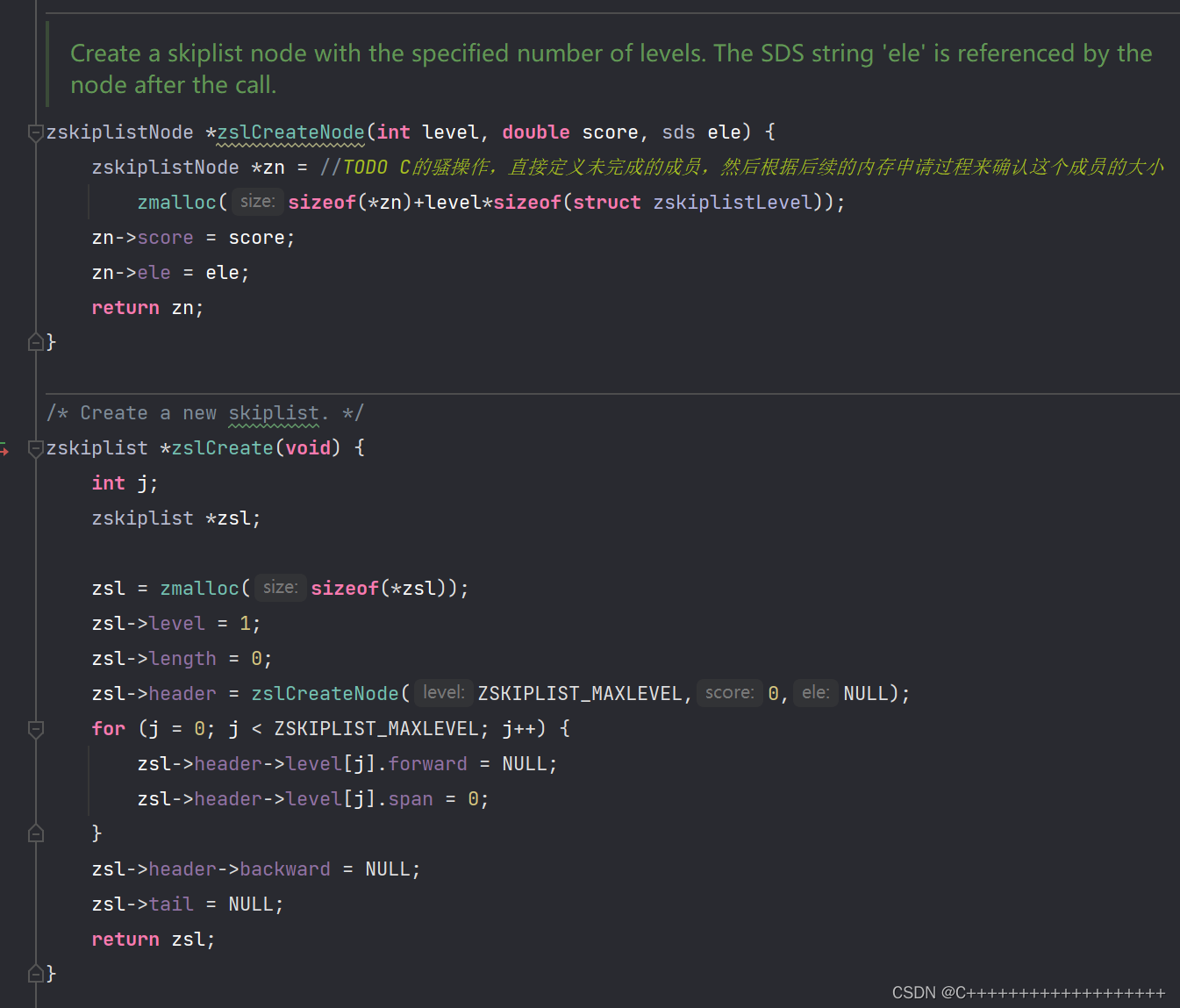
创建函数,这时前面定义的level[]类型的优势就体现出来了,在C中这个类型算是未完成的类型,所以需要根据你给它分配的内存来进行具体的使用,没有分配内存前,你可以sizeof(zskiplistNode);试一试,你会发现level不计内存!
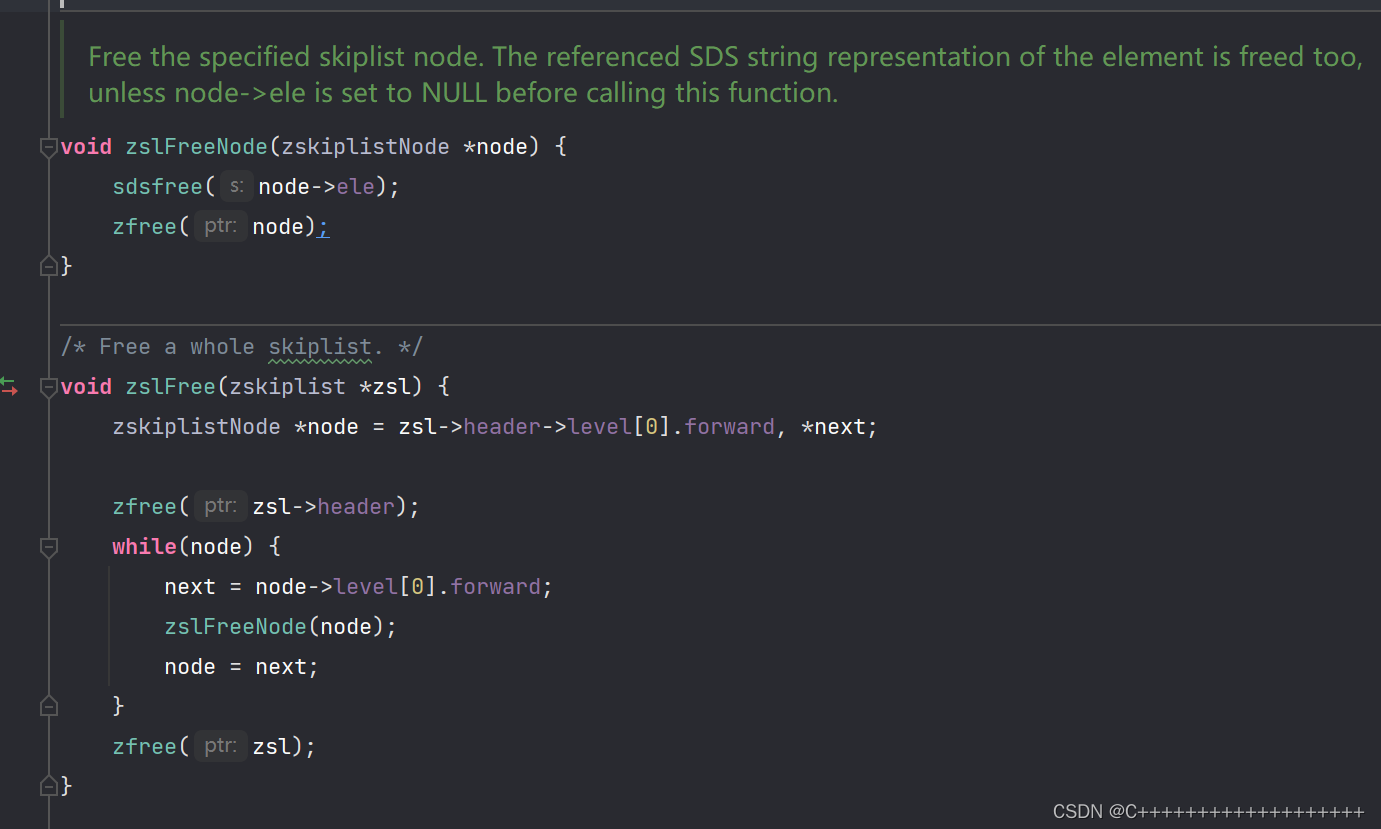
销毁函数
cpp实现
struct SkiplistNode {
// string ele; 此题不需要维护元素字段,所以舍去
double score;
SkiplistNode *backward;
struct SkiplistLevel {
struct SkiplistNode *forward;
// unsigned long span;此题不需要维护跨度,所以省去
}* level;
//TODO 构造和析构
SkiplistNode(int level,double score):level(new SkiplistLevel[level])
,score(score),backward(nullptr){}
~SkiplistNode(){
delete[] level;
}
};
class Skiplist {
struct SkiplistNode *header, *tail;
unsigned long length; //当前跳表中的元素个数
int level; //当前跳表中最大表的高度
public:
/**
* 构造函数和析构函数
*/
Skiplist():level(1),length(0),tail(nullptr){
header = new SkiplistNode(Skiplist_MAXLEVEL,0);
for (int j = 0; j < Skiplist_MAXLEVEL; j++) {
header->level[j].forward = nullptr;
}
header->backward = nullptr;
}
~Skiplist(){
SkiplistNode* node = header, *next;
while(node) {
next = node->level[0].forward;
delete node;
node = next;
}
}
};
Insert插入元素
Redis实现
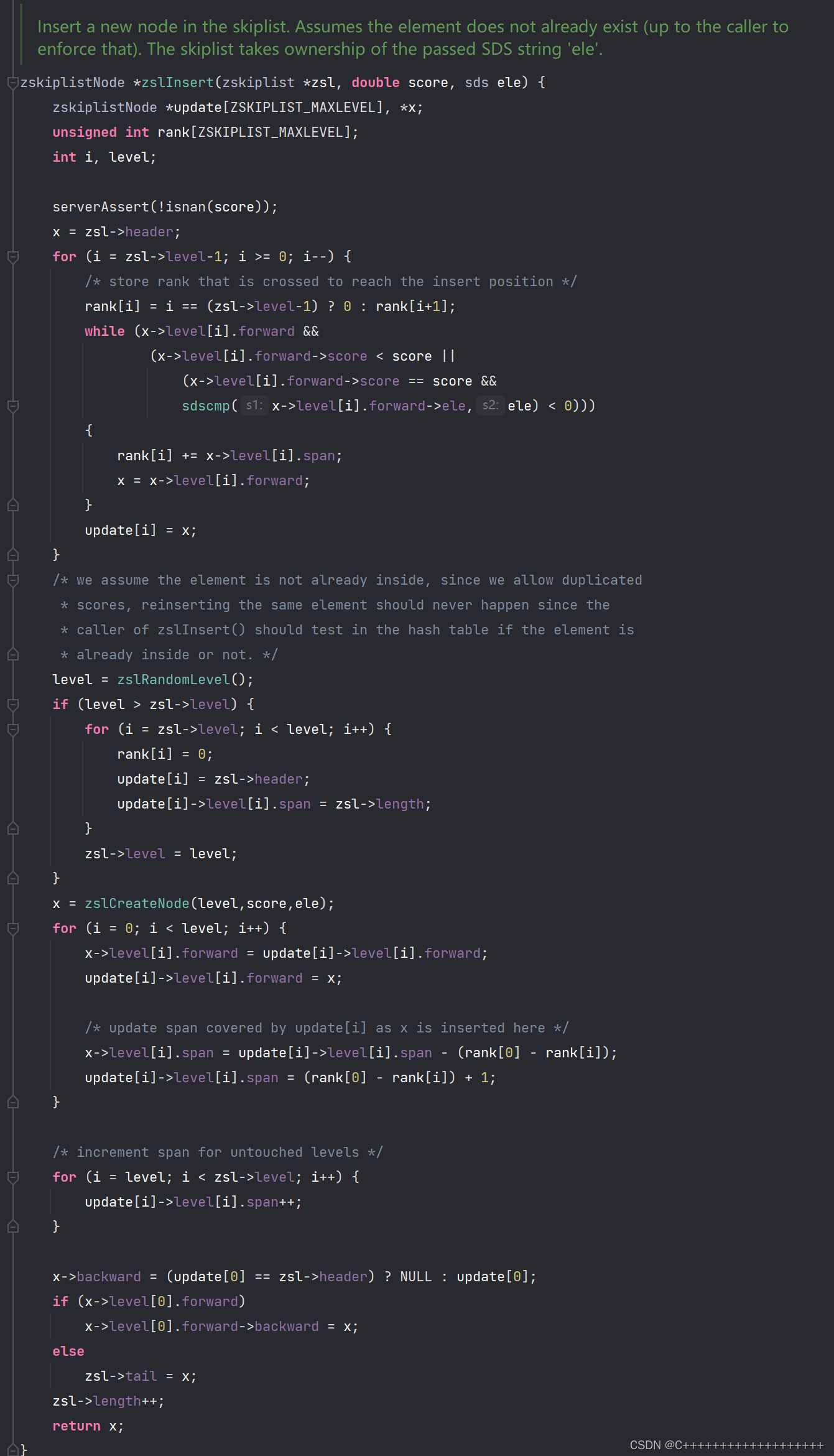
cpp实现
带span和ele的1:1还原
SkiplistNode* Skiplist::Insert(double score,const string& ele){
SkiplistNode *update[Skiplist_MAXLEVEL], *x;
unsigned int rank[Skiplist_MAXLEVEL];
int i,level;
//TODO part1:找到需要插入位置的前一个跳表节点,顺便更新update数组(存储着经过路径中的每个层级最多走到了哪个节点(用于连接新节点的每个层级的forward和更新span))和rank数组(存储着路径中经过的层级节点到header的长度)
x = header;
for (i = this->level-1; i >= 0; i--) {
rank[i] = i == (this->level-1) ? 0 : rank[i+1];
cout<<rank[i]<<endl;
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
x->level[i].forward->ele<ele)))
{
rank[i] += x->level[i].span;
x = x->level[i].forward;
}
update[i] = x;
}
//TODO 生成节点内存,如果随机生成的节点拥有的层级比当前最高的节点还高,则需要把update数组和rank数组中高于当前level的部分看作是前一个节点是header来更新
level = RandomLevel();
if (level > this->level) {
for (i = this->level; i < level; i++) {
rank[i] = 0;
update[i] = this->header;
update[i]->level[i].span = this->length;
}
this->level = level;
}
x = new SkiplistNode(level,score,ele);
//TODO 连接操作,连接的同时把上一个节点的span给转移给我,如果该层级的上一个节点就紧挨着那么可直接转移,否则根据update[i]->level[i].span - (rank[0] - rank[i]);来更新,实际上也包含了前一种情况
for (i = 0; i < level; i++) {
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
/* update span covered by update[i] as x is inserted here */
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
//TODO 最后的善后操作,1.前面高于它的节点,会因为它的产生而使得它们的span+1. 2.更新backward指针,如果不是队尾则需要更新后面的backward,如果插入的是队尾,则更新tail指针 3.更新length
/**
* 更新插入的节点未能到达的元素的span+1
*/
for (i = level; i < this->level; i++) {
update[i]->level[i].span++;
}
/**
* 更新backward,以及判断插入元素是否是队尾,如果是,则更新tail指针
*/
x->backward = (update[0] == this->header) ? nullptr : update[0];
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
this->tail = x;
this->length++;
return x;
}
不带span和ele
SkiplistNode* Skiplist::Insert(double score){
SkiplistNode *update[Skiplist_MAXLEVEL], *x;
int i,level;
//TODO part1:找到需要插入位置的前一个跳表节点,顺便更新update数组(存储着经过路径中的每个层级最多走到了哪个节点(用于连接新节点的每个层级的forward))
x = this->header;
for (i = this->level-1; i >= 0; i--) {
while (x->level[i].forward&&
x->level[i].forward->score < score)
{
x = x->level[i].forward;
}
update[i] = x;
}
//TODO 生成节点内存,如果随机生成的节点拥有的层级比当前最高的节点还高,则需要把update数组中高于当前level的部分看作是前一个节点是header来更新
level = RandomLevel();
if (level > this->level) {
for (i = this->level; i < level; i++) {
update[i] = this->header;
}
this->level = level;
}
x = new SkiplistNode(level,score);
//TODO 连接操作
for (i = 0; i < level; i++) {
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
}
/**
* 更新backward,以及判断插入元素是否是队尾,如果是,则更新tail指针
*/
x->backward = (update[0] == this->header) ? nullptr : update[0];
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
this->tail = x;
this->length++;
return x;
}
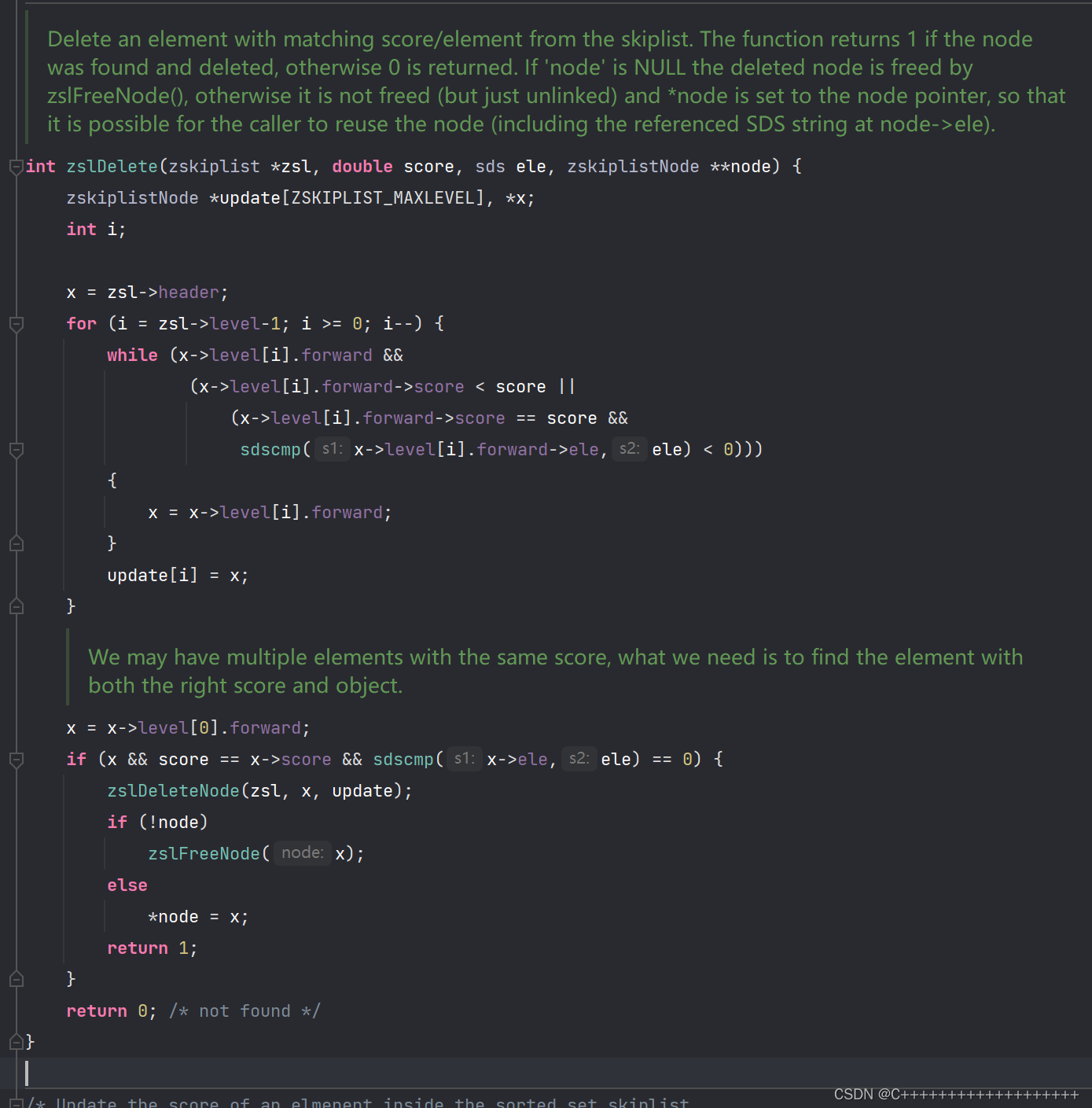
Delete删除元素
Redis实现
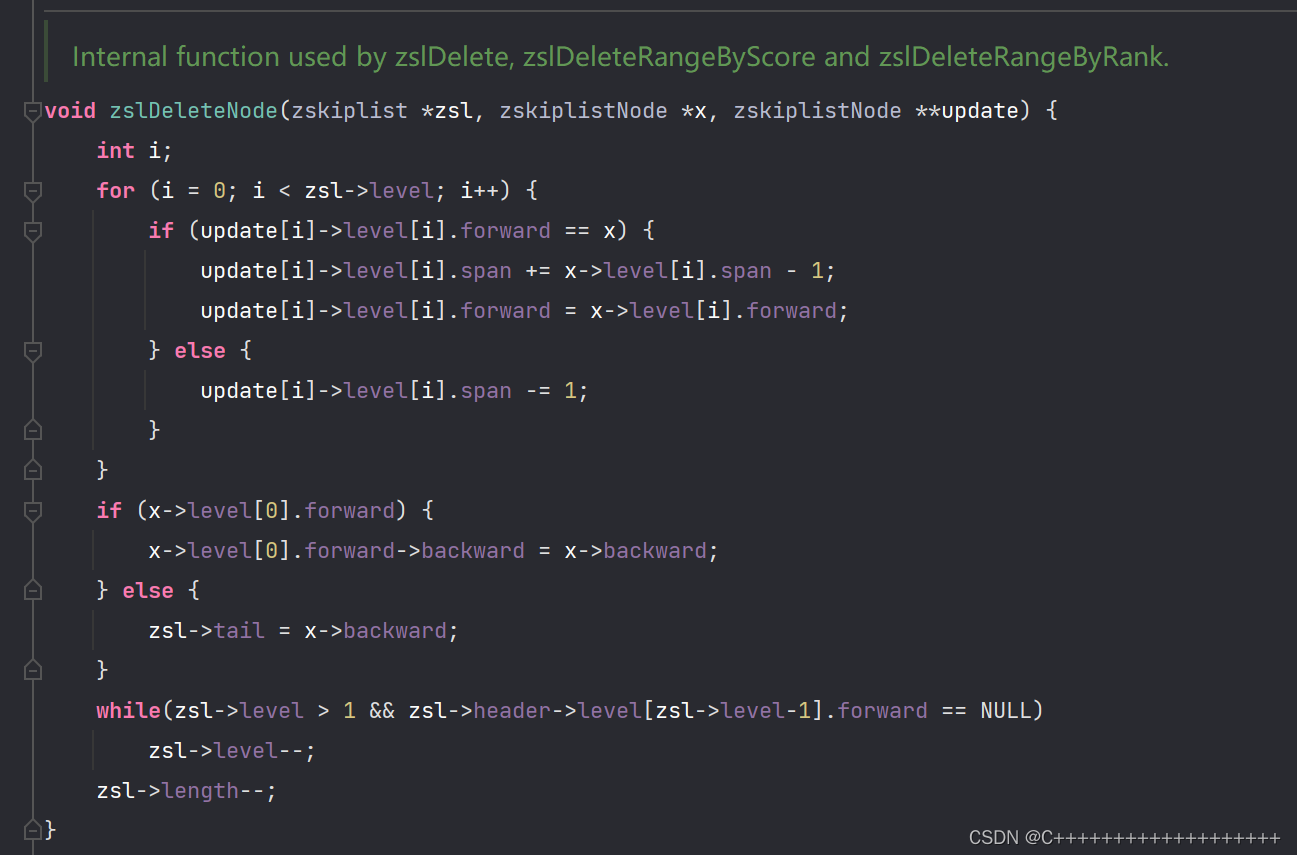
delete的helper函数
正式delete
cpp实现
1:1还原实现
/**
* 该函数处理传入的update数组,并更新删除x节点后的指针连接和span值
* @param zsl 需要处理的跳表
* @param x 需要删除的节点
* @param update 需要处理的的update数组
*/
static void Skiplist::DeleteNode(Skiplist *zsl, SkiplistNode *x, SkiplistNode **update) {
int i;
for (i = 0; i < zsl->level; i++) {
if (update[i]->level[i].forward == x) {//TODO 如果该层级的节点的后一个节点就是x节点,那么删除x节点后span会增加,forward要更新
update[i]->level[i].span += x->level[i].span - 1;
update[i]->level[i].forward = x->level[i].forward;
} else {//TODO 如果后一个节点不是x节点,那么就仅仅只是跨度上减少1而已
update[i]->level[i].span -= 1;
}
}
//TODO 和之前的插入处理相同,如果删除的节点是末尾节点,则需要更新tail指针,如果不是,则需要更新backward指针
if (x->level[0].forward) {
x->level[0].forward->backward = x->backward;
} else {
zsl->tail = x->backward;
}
while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
zsl->level--;
zsl->length--;
}
/**
* 根据score和ele删除节点
* @param score 传入的分值标识
* @param ele 传入的元素字符串标识
* @param node 用于选择是否要传出node,而不是就地删除
* @return 0表示节点未找到,1表示删除处理成功
*/
int Skiplist::Delete( double score, string ele, SkiplistNode **node = nullptr) {
SkiplistNode *update[Skiplist_MAXLEVEL], *x;
int i;
x = this->header;
for (i = this->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
x->level[i].forward->ele<ele)))
{
x = x->level[i].forward;
}
update[i] = x;
}
/**
* 我们可能有多个相同分数的元素,我们需要找到同时具有正确分数和对象的元素。
*/
x = x->level[0].forward;
if (x && score == x->score && x->ele==ele) {
DeleteNode(this, x, update);//TODO 处理update数组上的指针连接
if (!node)//TODO 如果外界不需要接住node来进行处理,则该node就地销毁,否则资源传出到外界
delete x;
else
*node = x;
return 1;
}
return 0; /* not found */
}
仅包含score的还原
/**
* 删除节点后的处理过程
* @param zsl 需要处理的跳表
* @param x 需要删除的节点
* @param update 需要处理的update数组
*/
static void Skiplist::DeleteHelper(Skiplist *zsl, SkiplistNode *x, SkiplistNode **update) {
assert(zsl!= nullptr&&x!= nullptr&&update!= nullptr);
int i;
for (i = 0; i < zsl->level; i++) {
if (update[i]->level[i].forward == x) {
update[i]->level[i].forward = x->level[i].forward;
}
}
//TODO 和之前的插入处理相同,如果删除的节点是末尾节点,则需要更新tail指针,如果不是,则更新backward指针
if (x->level[0].forward) {
x->level[0].forward->backward = x->backward;
} else {
zsl->tail = x->backward;
}
//TODO 删除的节点可能是最高的高度,由于可能存在多个相同的高度,所以我们不能直接判断
// 可从头节点的forward指针是否为空来确认高度是否需要下降
while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == nullptr)
zsl->level--;
zsl->length--;
}
/**
* 根据score和ele删除节点
* @param score 传入的分值标识
* @param node 用于选择是否要传出node,而不是就地删除
* @return 0表示节点未找到,1表示删除处理成功
*/
int Skiplist::Delete( double score,SkiplistNode **node = nullptr) {
SkiplistNode *update[Skiplist_MAXLEVEL], *x;
int i;
/**
* 查找并更新update数组
*/
x = this->header;
for (i = this->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < score))
{
x = x->level[i].forward;
}
update[i] = x;
}
x = x->level[0].forward;
if (x && score == x->score) {
DeleteHelper(this, x, update);//TODO 处理update数组上的指针连接
if (!node)//TODO 如果外界不需要接住node来进行处理,则该node就地销毁,否则资源传出到外界
delete x;
else
*node = x;
return 1;
}
return 0; /* not found */
}
正式解题
前面的增删弄懂了,这个跳表的各种查找也就不在话下了,现在可以正式解题了。 效率还是比较nice的!
解题源码:
#define Skiplist_MAXLEVEL 32 /* Should be enough for 2^64 elements */
#define Skiplist_P 0.25 /* Skiplist P = 1/4 */
struct SkiplistNode {
// string ele; 此题不需要维护元素字段,所以舍去
double score;
SkiplistNode *backward;
struct SkiplistLevel {
struct SkiplistNode *forward;
// unsigned long span;此题不需要维护跨度,所以省去
}* level;
SkiplistNode(int level,double score):level(new SkiplistLevel[level])
,score(score),backward(nullptr){}
~SkiplistNode(){
delete[] level;
}
};
class Skiplist {
public:
struct SkiplistNode *header, *tail;
unsigned long length; //当前跳表中的元素个数
int level; //当前跳表中最大表的高度
private:
/**
*
* @return 返回随机产生的level高度
*/
static int RandomLevel() {//TODO 根据rand()和掩码相与得到对应的随机值(0,0xffff)来产生level
int level = 1;
while ((rand()&0xFFFF) < (Skiplist_P * 0xFFFF))
level += 1;
return (level<Skiplist_MAXLEVEL) ? level : Skiplist_MAXLEVEL;
}
/**
* 删除节点后的处理过程
* @param zsl 需要处理的跳表
* @param x 需要删除的节点
* @param update 需要处理的update数组
*/
static void DeleteHelper(Skiplist *zsl, SkiplistNode *x, SkiplistNode **update) {
assert(zsl!= nullptr&&x!= nullptr&&update!= nullptr);
int i;
for (i = 0; i < zsl->level; i++) {
if (update[i]->level[i].forward == x) {
update[i]->level[i].forward = x->level[i].forward;
}
}
//TODO 和之前的插入处理相同,如果删除的节点是末尾节点,则需要更新tail指针,如果不是,则更新backward指针
if (x->level[0].forward) {
x->level[0].forward->backward = x->backward;
} else {
zsl->tail = x->backward;
}
//TODO 删除的节点可能是最高的高度,由于可能存在多个相同的高度,所以我们不能直接判断
// 可从头节点的forward指针是否为空来确认高度是否需要下降
while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == nullptr)
zsl->level--;
zsl->length--;
}
public:
/**
* 构造函数和析构函数
*/
Skiplist():level(1),length(0),tail(nullptr){
header = new SkiplistNode(Skiplist_MAXLEVEL,0);
for (int j = 0; j < Skiplist_MAXLEVEL; j++) {
header->level[j].forward = nullptr;
}
header->backward = nullptr;
}
~Skiplist(){
SkiplistNode* node = header, *next;
while(node) {
next = node->level[0].forward;
delete node;
node = next;
}
}
/**
* 插入元素
* @param score 用于定位的score
* @param ele 存储的元素
* @return 被插入元素的指针
*/
SkiplistNode* Insert(double score){
SkiplistNode *update[Skiplist_MAXLEVEL], *x;
int i,level;
//TODO part1:找到需要插入位置的前一个跳表节点,顺便更新update数组(存储着经过路径中的每个层级最多走到了哪个节点(用于连接新节点的每个层级的forward))
x = header;
for (i = this->level-1; i >= 0; i--) {
while (x->level[i].forward&&
x->level[i].forward->score < score)
{
x = x->level[i].forward;
}
update[i] = x;
}
//TODO 生成节点内存,如果随机生成的节点拥有的层级比当前最高的节点还高,则需要把update数组中高于当前level的部分看作是前一个节点是header来更新
level = RandomLevel();
if (level > this->level) {
for (i = this->level; i < level; i++) {
update[i] = this->header;
}
this->level = level;
}
x = new SkiplistNode(level,score);
//TODO 连接操作
for (i = 0; i < level; i++) {
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
}
/**
* 更新backward,以及判断插入元素是否是队尾,如果是,则更新tail指针
*/
x->backward = (update[0] == this->header) ? nullptr : update[0];
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
this->tail = x;
this->length++;
return x;
}
/**
* 根据score和ele删除节点
* @param score 传入的分值标识
* @param node 用于选择是否要传出node,而不是就地删除
* @return 0表示节点未找到,1表示删除处理成功
*/
int Delete( double score,SkiplistNode **node = nullptr) {
SkiplistNode *update[Skiplist_MAXLEVEL], *x;
int i;
/**
* 查找并更新update数组
*/
x = this->header;
for (i = this->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < score))
{
x = x->level[i].forward;
}
update[i] = x;
}
x = x->level[0].forward;
if (x && score == x->score) {
DeleteHelper(this, x, update);//TODO 处理update数组上的指针连接
if (!node)//TODO 如果外界不需要接住node来进行处理,则该node就地销毁,否则资源传出到外界
delete x;
else
*node = x;
return 1;
}
return 0; /* not found */
}
//本题的函数接口
bool search(int target) const {
double score = target;
SkiplistNode* x;
int i;
x = this->header;
for (i = this->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < score))
{
x = x->level[i].forward;
}
}
auto val = x->level[0].forward;
if(val)
return val->score==score;
return false;
}
void add(int num) {
Insert(double(num));
}
bool erase(int num) {
return Delete(double(num));
}
};