k站中转内最便宜的航班--BellmanFord算法和SPFA算法的改造
目录
题目
BellmanFord算法的动态规划解决(效率一般)

看到k站内,肯定会想到
BellmanFord算法的动态规划解法,本来优化成按边遍历的动态规划可以不用计较多少次,但这里必须要计较用了多少次,所以我们要在同一次边的选择中,保证另一个边用的是上一次的结果,故通过二维数组进行dp即可写出,要压缩成一维数组也不难,毕竟用的仅仅只是上一行的结果,所以动态规划解决是非常简单的。
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
const int INF = 0x3f3f3f3f;
//用临时数组存储,这样改变了dist也不会改变temp,这样便达到了控制遍历次数的目的
int* dist = new int[n];
memset(dist,0x3f,sizeof(int)*n);
dist[src] = 0;
int sz = flights.size();
for(int i=0;i<=k;i++){
int* temp = new int[n];
memcpy(temp,dist,n*sizeof(int));
for(int j=0;j<sz;j++){
if(temp[flights[j][0]]!=INF){
dist[flights[j][1]] = min(dist[flights[j][1]],temp[flights[j][0]] + flights[j][2]);
}
}
delete[] temp;
}
return dist[dst]==INF?-1:dist[dst];
}
};
SPFA算法改造成为经典BFS解决(效率高)
为了效率,我建图时候用了链式前向星。
这道题开始拿到的时候,我就再想这个SPFA类似于BFS,那肯定是可以控制次数的,然后就开始行动了,SPFA队列遍历的时候需要判断该结点是否存在于队列中,如果存在,则不能入队,使用的数据都是通过
dist数组来更新,这样导致完全丧失了BFS的遍历次数信息,使得答案更新的很快是没错,但无法控制在一定的遍历次数范围内(因为可能你本次所用到的dist可能不是上一次的)。
那么如何解决这个 BFS 遍历次数的限制问题呢?
为了解决 SPFA 算法的这个问题我试了两种方式,只有最后有一种是可行的:
- (错误)利用同等长度的临时数组记录此次遍历后dist数组更新的结果,然后在遍历完的尾部利用该数组对
dist数组进行更新。
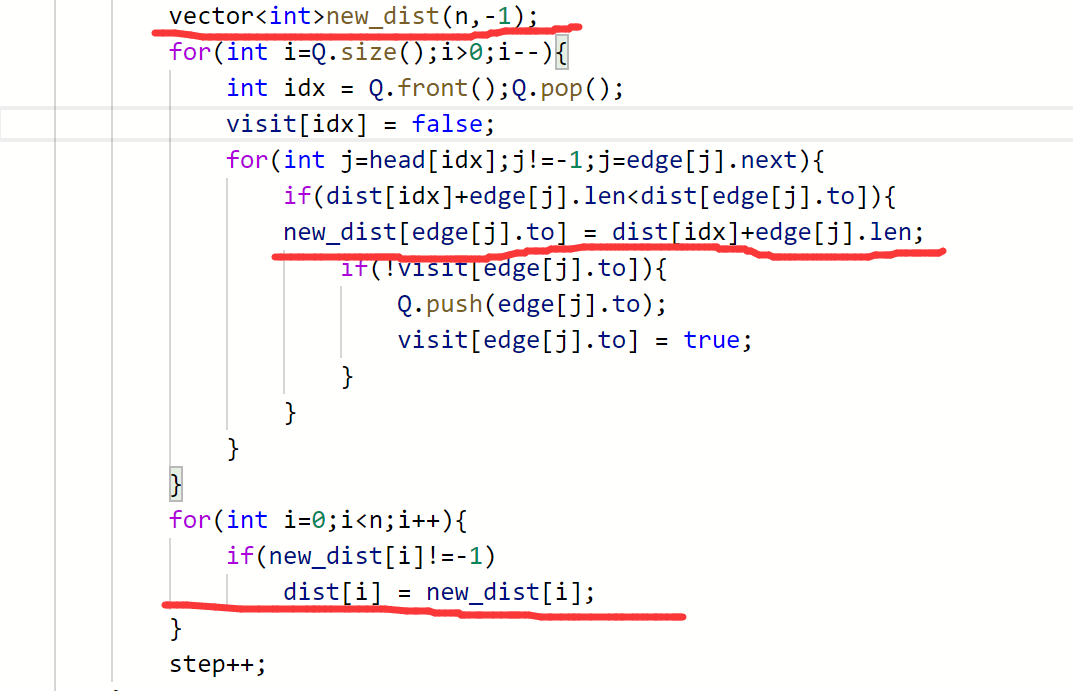
就像这样:
但很快会发现出现一个问题:一次遍历途中可能一个结点更新多次,那么这样就无法保证把所有k次中转内的情况都列举出来。
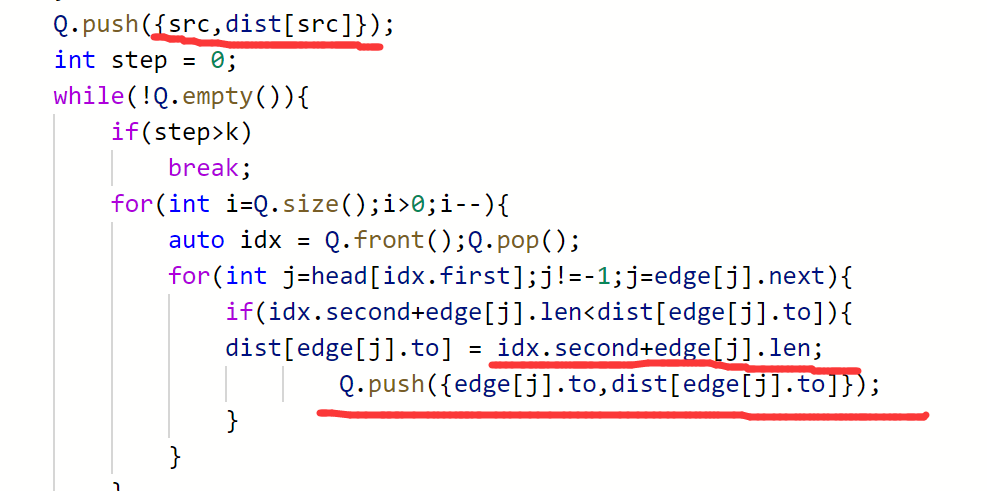
- (正确)利用队列的参数对dist进行更新,如何更新呢?队列中记录每个结点的
编号和到src的距离,每次更新新的dist的时候直接用正在遍历的编号到src的距离替代直接使用dist数组(这样便防止了更新dist数组后影响后续更新)。 如图:
解题代码:
class Solution {
public:
//用于建图的结构体
struct {
int to;
int len;
int next;
}edge[5000];
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
const int INF = 0x3f3f3f3f;
memset(head, 0xff, sizeof head);
int dist[n];memset(dist,0x3f,sizeof dist);
dist[src] = 0;
queue<pair<int,int>>Q;
int sz = flights.size();
for(int i=0;i<sz;i++){
add(flights[i][0],flights[i][1],flights[i][2]);
}
Q.push({src,dist[src]});
int step = 0;
while(!Q.empty()){
if(step>k)
break;
for(int i=Q.size();i>0;i--){
auto idx = move(Q.front());Q.pop();
for(int j=head[idx.first];j!=-1;j=edge[j].next){
if(idx.second+edge[j].len<dist[edge[j].to]){
dist[edge[j].to] = idx.second+edge[j].len;
Q.push({edge[j].to,dist[edge[j].to]});
}
}
}
step++;
}
if(dist[dst]!=INF)return dist[dst];
return -1;
}
private:
//用于链式前向星建图的函数和数据
int tot = 0;
int head[100];
void add(int node,int to,int len){
edge[tot].to = to;
edge[tot].len = len;
edge[tot].next = head[node];
head[node] = tot;
tot++;
}
};

 但很快会发现出现一个问题:一次遍历途中可能一个结点更新多次,那么这样就无法保证把所有k次中转内的情况都列举出来。
但很快会发现出现一个问题:一次遍历途中可能一个结点更新多次,那么这样就无法保证把所有k次中转内的情况都列举出来。