
并查集/dfs解决——leetcode每日一题——1020飞地的数量
目录
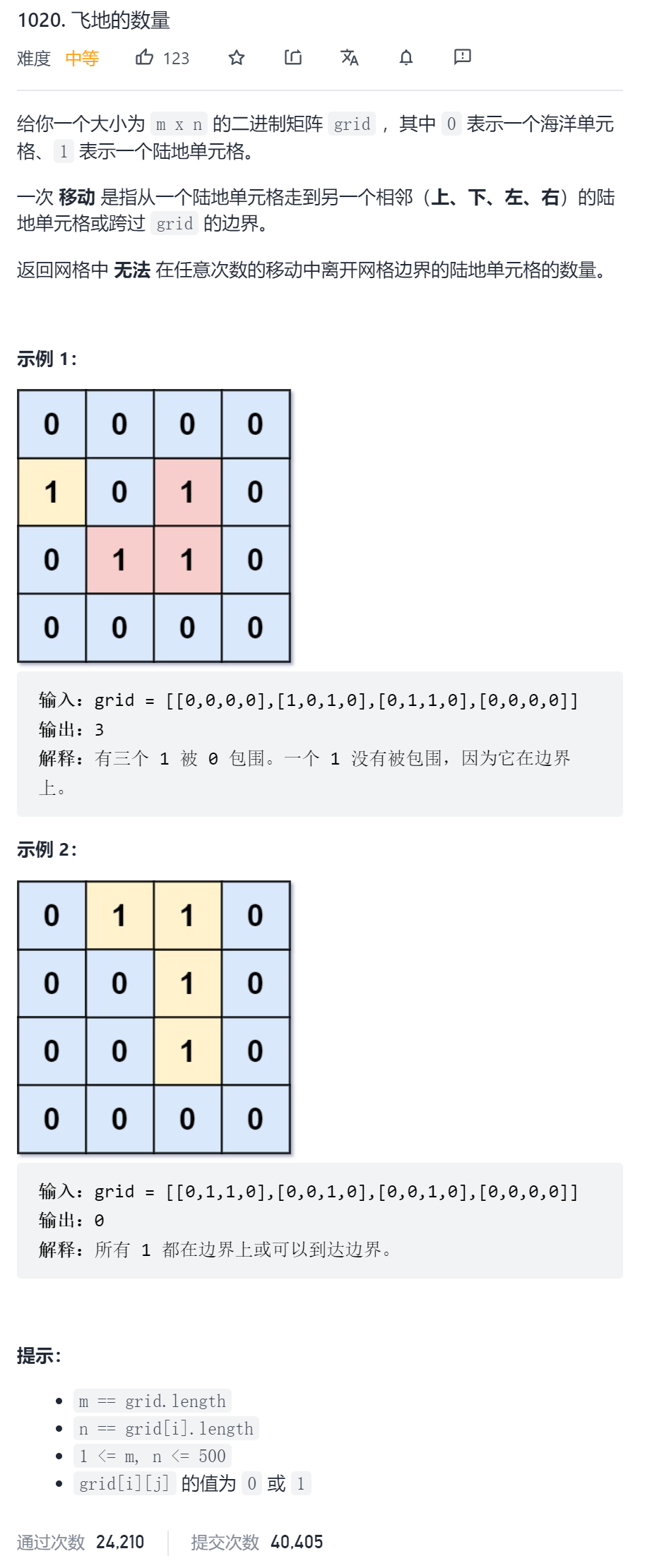
题目描述
题目解析
一、以边界值为对象进行搜索解决
一开始很快就想到用比较暴力的直接dfs深搜,然后就超时了。
注意此题由于以 1 是否能延申到整个边界以外来判断是否为有效的 1 所以我们需要取巧,应该以所有边界的 1 为对象先把所有能超出的 1 搜出来,然后剩余的 1 就是答案了。
二、并查集合并+是否接壤边界属性更新
创建一个并查集,用一维数组存下所有二维数组的元素,同时再增加一个一维数组用于判断是否边界接壤,每次 merge 操作的时候判断需要同时执行合并操作和是否接壤的更新。
先利用并查集 merge 所有的 1,然后再挨个判断是否接壤即可。
解题代码
dfs方法:
class Solution {
public:
vector<vector<int>> dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int numEnclaves(vector<vector<int>>& grid) {
this->m = grid.size();
this->n = grid[0].size();
this->visited = vector<vector<bool>>(m, vector<bool>(n, false));
for (int i = 0; i < m; i++) {
dfs(grid, i, 0);
dfs(grid, i, n - 1);
}
for (int j = 1; j < n - 1; j++) {
dfs(grid, 0, j);
dfs(grid, m - 1, j);
}
int enclaves = 0;
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (grid[i][j] == 1 && !visited[i][j]) {
enclaves++;
}
}
}
return enclaves;
}
void dfs(const vector<vector<int>> & grid, int row, int col) {
if (row < 0 || row >= m || col < 0 || col >= n || grid[row][col] == 0 || visited[row][col]) {
return;
}
visited[row][col] = true;
for (auto & dir : dirs) {
dfs(grid, row + dir[0], col + dir[1]);
}
}
private:
int m, n;
vector<vector<bool>> visited;
};
并查集方法:
//这个并查集写的好
class UnionFind {
public:
UnionFind(const vector<vector<int>> & grid) {
int m = grid.size(), n = grid[0].size();
this->parent = vector<int>(m * n); //存储并查集的联通关系
this->onEdge = vector<bool>(m * n, false);//查找是否有在边界元素的关键所在
this->rank = vector<int>(m * n);
for (int i = 0; i < m; i++) { //根据传过来的二维数组更新并查集,同时更新onEdge边界元素为true
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
int index = i * n + j;
parent[index] = index;
if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
onEdge[index] = true;
}
}
}
}
}
int find(int i) {
if (parent[i] != i) {
parent[i] = find(parent[i]);
}
return parent[i];
}
void uni(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (rank[rootx] > rank[rooty]) {//这里时按秩优化处理
parent[rooty] = rootx;
onEdge[rootx] = onEdge[rootx] | onEdge[rooty];//每次合并元素的时候同时把这一堆是否与边界接壤的关系更新
} else if (rank[rootx] < rank[rooty]) {
parent[rootx] = rooty;
onEdge[rooty] = onEdge[rooty] | onEdge[rootx];
} else {
parent[rooty] = rootx;
onEdge[rootx] = onEdge[rootx] | onEdge[rooty];
rank[rootx]++;
}
}
}
bool isOnEdge(int i) {
return onEdge[find(i)];
}
private:
vector<int> parent; //并查集的必备
vector<bool> onEdge; //判断是否接壤边界
vector<int> rank; //按秩
};
class Solution {
public:
int numEnclaves(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
UnionFind uf(grid);
//先把所有的1连接起来,然后再判断是否接壤边界即可
//由于循环是从上往下,从左往右,故左和上方向不需要考虑
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
int index = i * n + j;
if (j + 1 < n && grid[i][j + 1] == 1) {
uf.uni(index, index + 1);
}
if (i + 1 < m && grid[i + 1][j] == 1) {
uf.uni(index, index + n);
}
}
}
}
//判断这个1是否和边界接壤
int enclaves = 0;
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (grid[i][j] == 1 && !uf.isOnEdge(i * n + j)) {
enclaves++;
}
}
}
return enclaves;
}
};